题目内容
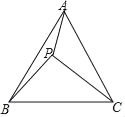
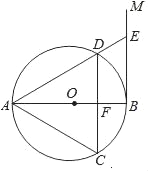
【题目】如图,已知PA、PB是⊙O的切线,A、B分别为切点,∠OAB=30°.
(1)∠APB=_____;
(2)当OA=2时,AP=_____.
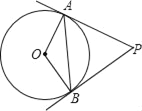
【答案】60° 2![]() .
.
【解析】
(1)根据四边形的内角和为360°,根据切线的性质可知:∠OAP=∠OBP=90°,求出∠AOB的度数,可将∠APB的度数求出;
(2)作辅助线,连接OP,在Rt△OAP中,利用三角函数,即可求出AP的长
(1)∵在△ABO中,OA=OB,∠OAB=30°,
∴∠AOB=180°﹣2×30°=120°,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°,
∴在四边形OAPB中,
∠APB=360°﹣120°﹣90°﹣90°=60°,
故答案为:60°.
(2)如图,连接OP;
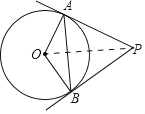
∵PA、PB是⊙O的切线,
∴PO平分∠APB,即∠APO=![]() ∠APB=30°,
∠APB=30°,
又∵在Rt△OAP中,OA=3,∠APO=30°,
∴AP=![]() =
=![]() = 2
= 2![]()
故答案为:2![]() .
.

【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
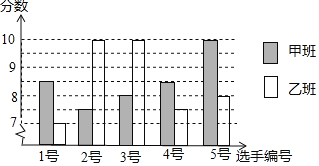
![]() 根据上图填写下表:
根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 |
|
| ______ | ______ |
乙班 |
| ______ | 10 |
|
![]() 根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
【题目】山西省地处中纬度,属于温带大陆性气候,因此适合种植玉米、高粱、大豆、花生等农作物,农民李大叔有一块总面积为![]() 的长方形种植地,为了便于农作物之间互传花粉,提高产量,计划分垄种植玉米和高粱(每垄种植一种农作物)共32垄,种植的每种农作物的垄数不低于14垄,又不超过18垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
的长方形种植地,为了便于农作物之间互传花粉,提高产量,计划分垄种植玉米和高粱(每垄种植一种农作物)共32垄,种植的每种农作物的垄数不低于14垄,又不超过18垄(垄数为正整数),它们的占地面积、产量、利润分别如下:


农作物 | 占地面积( | 产量(千克/垄) | 利润(元/千克) |
玉米 | 30 | 60 | 0.5 |
高粱 | 20 | 50 | 0.8 |
(1)若设高粱种植了![]() 垄,请说明共有几种种植方案,分别是哪几种;
垄,请说明共有几种种植方案,分别是哪几种;
(2)在以上种植方案中,哪种方案获得的利润最大?最大利润是多少?