题目内容
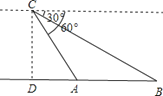
【题目】如图,各边长为 2 的等边三角形有一条 边在同一条直线上,设△B2D1C1 面 积为 S1,△B3D2C2 的面积为 S2,…,△B2019D2018C2018 的面积为 S2018,则 S2018=( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由图可知B1C1∥B2C2∥B3C3∥…∥BnCn,,因此有△AD1C1∽△AB2C2,△AD2C2∽△AB3C3,…这一系列的相似三角形的相似比是明显可求的,所以面积比也就可以知道了.以△AD1C1∽△AB2C2为例, △AB2C2的底为等边三角形边长的两倍,高与等边三角形的高相等,那么△AB2C2的面积就是等边三角形面的两倍,由于相似比为1:2,所以它们的面积比为1:4,从而可以求出△AD1C1的面积, △AB2C2的面积减去△AD1C1的面积和一个等边三角形的面积即是△B2D1C1的面积,后面的类推.
解:由等边三角形的边长为2可求解等边三角形的面积为![]() ,
,
∵△AD2017C2017∽△AB2018C2018,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
故选择C.

练习册系列答案
相关题目
【题目】在一个不透明的袋子中装有除颜色外其余均相同的m个小球,其中 5 个黑球, 从袋中随机摸出一球,记下其颜色,这称为依次摸球试验,之后把它放回袋 中,搅匀后,再继续摸出一球.以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
摸球试验次数 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
摸出黑球次数 | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
根据列表,可以估计出 m 的值是( )
A. 5 B. 10 C. 15 D. 20