题目内容
【题目】如图,已知矩形纸片ABCD中,AB=12,BC=16.将矩形纸片ABCD折叠,使点B与点D重合,点A折叠至点E处,GH为折痕,连接BG.
(1)△DGH是等腰三角形吗?请说明你的理由.
(2)求线段AG的长;
(3)求折痕GH的长.
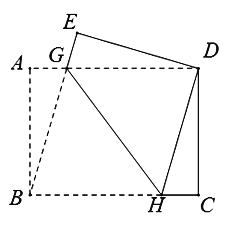
【答案】(1)△ DGH是等腰三角形,理由见解析;(2) AG=3.5;(3)折痕GH的长为15.
【解析】
(1)由翻折,找着重合的部分,得到相等的边,相等的角,再根据两直线平行,内错角相等可得即可证明;
(2)设出未知数,用未知数表示出相关的量,应用勾股定理,列出方程可求得答案.
(3)由(2)知BG=DG=16-3.5=12.5,因为 DG=DH=BH,GE∥DH,从而求出四边形BHDG是菱形,再利用勾股定理列式求出BD,然后根据菱形的面积列出方程求解即可.
(1)![]() DGH是等腰三角形,理由如下:在矩形ABCD中,∵AD∥BC,∴∠DGH=∠BHG,由折叠知∠DHG=∠BHG,∴∠DGH=∠DHG,∴DG=DH,即
DGH是等腰三角形,理由如下:在矩形ABCD中,∵AD∥BC,∴∠DGH=∠BHG,由折叠知∠DHG=∠BHG,∴∠DGH=∠DHG,∴DG=DH,即![]() DGH是等腰三角形;
DGH是等腰三角形;
(2)由折叠知AG=GE,设AG=x,则BG=DG=16-x,∵∠A=90°,![]() ,∴
,∴![]() ,解得x=3.5,∴AG=3.5;
,解得x=3.5,∴AG=3.5;
(3)由(2)知BG=DG=16-3.5=12.5,∵DG=DH=BH,GE∥DH,∴四边形BHDG是平行四边形,∴四边形BHDG是菱形.;
法一:作GF⊥BC于点F,则BF=AG=3.5,GF=AB=12,∴FH=BH-BF=12.5-3.5=9,
∴GH=![]() =
=![]() ,∴折痕GH的长为15.;
,∴折痕GH的长为15.;
法二:连接BD,则BD=![]() =
=![]() =20,∵四边形BHDG是菱形,
=20,∵四边形BHDG是菱形,
∴S菱形BHDG=BH·AB=![]() BD·GH,∴GH=
BD·GH,∴GH=![]() =15,∴折痕GH的长为15..
=15,∴折痕GH的长为15..

练习册系列答案
相关题目