Question

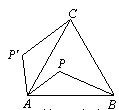
如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值是______________

Answer 1

10．

试题分析：由正方形性质的得出B、D关于AC对称，根据两点之间线段最短可知，连接DE，交AC于P，连接BP，则此时PB+PE的值最小，进而利用勾股定理求出即可．
试题解析：如图，连接DE，交AC于P，连接BP，则此时PB+PE的值最小．

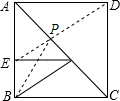
∵四边形ABCD是正方形，
∴B、D关于AC对称，
∴PB=PD，
∴PB+PE=PD+PE=DE．
∵BE=2，AE=3BE，
∴AE=6，AB=8，
∴DE=.
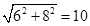故PB+PE的最小值是10．