题目内容
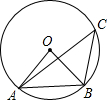如图，点A、B、C都在⊙O上，且点C在弦AB所对的优弧上，若∠ACB=38°，则∠AOB的度数是
- A.19°
- B.30°
- C.76°
- D.38°
C
分析：由∠ACB=38°，根据在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠AOB的度数．
解答：∵点A、B、C都在⊙O上，且点C在弦AB所对的优弧上，∠ACB=38°，
∴∠AOB=2∠ACB=2×38°=76°．
故选C．
点评：此题考查了圆周角定理．此题比较简单，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用是解此题的关键，注意数形结合思想的应用．
分析：由∠ACB=38°，根据在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠AOB的度数．
解答：∵点A、B、C都在⊙O上，且点C在弦AB所对的优弧上，∠ACB=38°，
∴∠AOB=2∠ACB=2×38°=76°．
故选C．
点评：此题考查了圆周角定理．此题比较简单，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用是解此题的关键，注意数形结合思想的应用．
练习册系列答案
相关题目
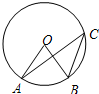11、如图，点A、B、C都在⊙O上，若∠C=35°，则∠AOB=
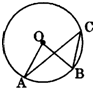13、如图，点A、B、C都在00上，若∠C=40°，则∠AOB的度数为（ ）
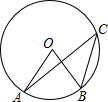（2013•丰台区二模）如图，点A、B、C都在⊙O上，若∠AOB=68°，则∠ACB的度数为（ ）
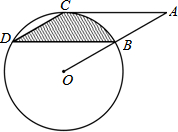（2013•自贡）如图，点B、C、D都在⊙O上，过点C作AC∥BD交OB延长线于点A，连接CD，且∠CDB=∠OBD=30°，DB=
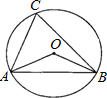如图，点A、B、C都在⊙O上，连接AB、BC、AC、OA、OB，且∠BAO=25°，则∠ACB的大小为