题目内容
 在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2+bx-c=0为“△ABC的☆方程”.根据规定解答下列问题:
在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2+bx-c=0为“△ABC的☆方程”.根据规定解答下列问题:(1)“△ABC的☆方程”ax2+bx-c=0的根的情况是
②
②
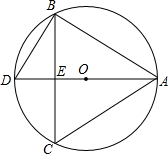
(填序号):①有两个相等的实数根;②有两个不相等的实数根;③没有实数根;(2)如图,AD为⊙O的直径,BC为弦,BC⊥AD于E,∠DBC=30°,求“△ABC的☆方程”ax2+bx-c=0的解;
(3)若x=
| 1 | 4 |
分析:(1)利用三角形各边大于0,再利用△=b2+4ac>0,得出答案即可;
(2)利用等边三角形的判定得出△ABC是等边三角形,进而得出a=b=c,求出方程的根即可;
(3)将x=
c代入☆方程中可得:
+
-c=0,进而化简得出ac+4b-16=0,结合ac-4b<0,可得出0<ac<8,进而求出a,b,c的值求出方程的根即可.
(2)利用等边三角形的判定得出△ABC是等边三角形,进而得出a=b=c,求出方程的根即可;
(3)将x=
| 1 |
| 4 |
| ac2 |
| 16 |
| bc |
| 4 |
解答:解:(1)∵在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,关于x的一元二次方程ax2+bx-c=0为“△ABC的☆方程”,
∴a>0,b>0,c>0,
∴△=b2+4ac>0,
∴方程有两个不相等的实数根.
故答案为:②;
(2)∵AD为⊙O的直径,
∴∠DBA=90°,
∵∠DBC=30°,
∴∠CBA=60°,
∵BC⊥AD于E,∠DBC=30°,
∴∠BDA=60°,
∴∠C=60°,
∴△ABC是等边三角形,
∴a=b=c,
∴“△ABC的☆方程”ax2+bx-c=0可以变为:ax2+ax-a=0,
∵△=b2+4ac>0,
∴x=
=
,
即x1=
,x2=
;
(3)将x=
c代入☆方程中可得:
+
-c=0,
方程两边同除以c可得:
+
-1=0,
化简可得:ac+4b-16=0,
结合ac-4b<0,可得出0<ac<8,
由ac+4b=16,可知ac需能被4整除,又0<ac<8;
∴ac=4,从而b=3,
又因为a,c为正整数,则a=1,c=4(不能构成三角形,舍去)或者a=c=2,
所以☆方程为2x2+3x-2=0,
解得:x1=
,x2=-2.
∴a>0,b>0,c>0,
∴△=b2+4ac>0,
∴方程有两个不相等的实数根.
故答案为:②;
(2)∵AD为⊙O的直径,
∴∠DBA=90°,
∵∠DBC=30°,
∴∠CBA=60°,
∵BC⊥AD于E,∠DBC=30°,
∴∠BDA=60°,
∴∠C=60°,
∴△ABC是等边三角形,
∴a=b=c,
∴“△ABC的☆方程”ax2+bx-c=0可以变为:ax2+ax-a=0,
∵△=b2+4ac>0,
∴x=
-a±
| ||
| 2a |
-1±
| ||
| 2 |
即x1=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
(3)将x=
| 1 |
| 4 |
| ac2 |
| 16 |
| bc |
| 4 |
方程两边同除以c可得:
| ac |
| 16 |
| b |
| 4 |
化简可得:ac+4b-16=0,
结合ac-4b<0,可得出0<ac<8,
由ac+4b=16,可知ac需能被4整除,又0<ac<8;
∴ac=4,从而b=3,
又因为a,c为正整数,则a=1,c=4(不能构成三角形,舍去)或者a=c=2,
所以☆方程为2x2+3x-2=0,
解得:x1=
| 1 |
| 2 |
点评:此题主要考查了根的判别式以及一元二次方程的解法和等边三角形的判定等知识,注意利用ac-4b<0,ac+4b-16=0得出a,c的值是解题关键.

练习册系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
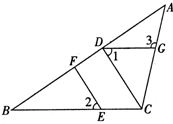 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
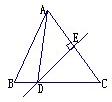 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于