Question

【题目】实验证明，平面镜反射光线的规律是：照射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．

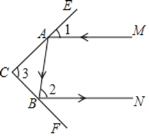
如图，一束光线MA照射到平面镜CE上，被CE反射到平面镜CF上，又被CF反射．已知被CF反射出的光线BN与光线MA平行．若∠1=35°，则∠2= ，∠3= ；若∠1=50°，∠3= ．

（2）由（1）猜想：当两平面镜CE，CF的夹角∠3为多少度时，可以使任何射到平面镜CE上的光线MA，经过平面镜CE，CF的两次反射后，入射光线MA与反射光线BN平行，请你写出推理过程．

Answer 1

【答案】（1）70°，90°，90°；（2）猜想：当两平面镜CE，CF的夹角∠3为90°时，可以使任何射到平面镜CE上的光线MA，经过平面镜CE，CF的两次反射后，入射光线MA与反射光线BN平行．理由见解析．

【解析】

（1）根据平行线的性质和三角形内角和，以及入射角等于反射角，可以求得∠2和∠3的度数；

（2）先写出∠3等于多少度，然后根据题意和图形结合第（1）问的提示思路，即可写出推理过程．

解：（1）∵AM∥BN，

∴∠MAB+∠2=180°，

∵∠MAB+∠1+∠BAC=180°，∠1=∠BAC，∠1=35°，

∴∠2=2∠1=70°，

∵∠2+∠ABC+∠NBF=180°，∠ABC=∠NBF，

∴∠ABC=55°，

∴∠3=180°-∠BAC-∠ABC=90°；

当∠1=50°时， 同理可得，∠2=100°，∠ABC=40°，∠BAC=∠1=50°，

则∠3=180°-∠BAC-∠ABC=90°；

故答案为：70°，90°，90°；

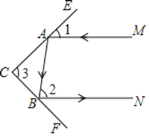
（2）猜想：当两平面镜CE，CF的夹角∠3为90°时，可以使任何射到平面镜CE上的光线MA，经过平面镜CE，CF的两次反射后，入射光线MA与反射光线BN平行．

理由：∵∠3=90°，

∴∠BAC+∠ABC=90°，

∵∠1=∠BAC，∠ABC=∠NBF，

∴∠BAC+∠1+∠ABC+∠NBF=180°，

∴∠MAB+∠2=180°，

∴MA∥BN．