��Ŀ����
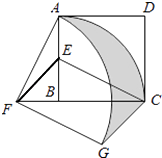
����Ŀ��(12��)�������������ֲ�ͬ�ķ�������ͬһͼ�ε����ʱ�����Եõ�һ����ʽ�����磬��ͼ�٣��ɵõ�ʽ��(a��2b)(a��b)��a2��3ab��2b2.
(1)��ͼ�ڣ��ɵõ�ʽ��__________________________��
(2)����(1)�����õ��Ľ��ۣ������������⣺
��֪a��b��c��11��ab��bc��ac��38����a2��b2��c2��ֵ��
(3)����ͼ���е�ֽƬ(�㹻��)������һ��ƴͼ��ʹ��ƴͼ��������֤��ʽ��2a2��5ab��2b2��(2a��b)(a��2b);
(4)������2�ű߳�Ϊa�������Σ�3�ű߳�Ϊb�������Σ�5�ű߳��ֱ�Ϊa��b�ij�����ֽƬ����ƴ��һ�������Σ���ô�ó����νϳ���һ���߳�Ϊ________��

���𰸡�(1)(a��b��c)2��a2��b2��c2��2ab��2ac��2bc;(2)45;(3)�𰸼�����;(4) 2a��3b.
�������������������1��.����ͼ2������ֱ�������ӷ��ֱ��ʾ�����������������ȷ���������ʽ����2��.���ݣ�1���еĵ�ʽ�����б��Σ��������ʽ�ӵ�ֵ���ɣ���3��.������֪��ʽ��������Ϊ2a+b����Ϊa+2b�ij�����ͼ�μ��ɣ���4��.��������֪ͼ�ε������2a2+5ab+3b2���г���ϵʽ2a2+5ab+3b2=(2a+3b)(a+b)������ȷ���������νϳ��ı�.
�⣺(1)(a��b��c)2��a2��b2��c2��2ab��2ac��2bc.
(2)��a��b��c��11��ab��bc��ac��38����a2��b2��c2��(a��b��c)2��2(ab��ac��bc)��112��2��38��45.
(3)��ͼ��ʾ��
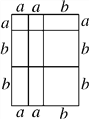
(4)��������ã�2a2+5ab+3b2=(2a+3b)(a+b)��
��ϳ���һ��Ϊ2a+3b.