题目内容
解方程
(1)x2-3x+1=0
(2)x2-5x-6=0.
(1)解:x2-3x+1=0,
这里a=1,b=-3,c=1,
b2-4ac=(-3)2-4×1×1=5,
∴x=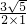 ,
,
∴方程的解是 .
.
(2)解:x2-5x-6=0,
分解因式得:(x-6)(x+1)=0,
∴x-6=0,x+1=0,
解方程得:x1=6,x2=-1,
∴方程的解是x1=6,x2=-1.
分析:(1)求出b2-4ac=5,代入公式x=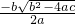 求出即可;
求出即可;
(2)分解因式得到(x-6)(x+1)=0,推出方程x-6=0,x+1=0,求出方程的解即可.
点评:本题主要考查对解一元二次方程-因式分解法、公式法,解一元一次方程等知识点的理解和掌握,能选择适当的方法解一元二次方程是解此题的关键.
这里a=1,b=-3,c=1,
b2-4ac=(-3)2-4×1×1=5,
∴x=
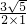 ,
,∴方程的解是
 .
.(2)解:x2-5x-6=0,
分解因式得:(x-6)(x+1)=0,
∴x-6=0,x+1=0,
解方程得:x1=6,x2=-1,
∴方程的解是x1=6,x2=-1.
分析:(1)求出b2-4ac=5,代入公式x=
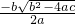 求出即可;
求出即可;(2)分解因式得到(x-6)(x+1)=0,推出方程x-6=0,x+1=0,求出方程的解即可.
点评:本题主要考查对解一元二次方程-因式分解法、公式法,解一元一次方程等知识点的理解和掌握,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
解方程
+
=3时.设y=
,则原方程化为y的整式方程为( )
| x |
| x2-1 |
| 2(x2-1) |
| x |
| x |
| x2-1 |
| A、2y2-6y+1=0 |
| B、y2-3y+2=0 |
| C、2y2-3y+1=0 |
| D、y2+2y-3=0 |