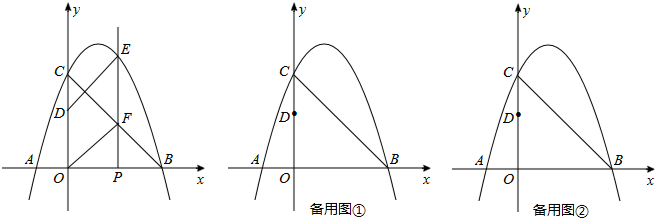
��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У���ֱ��y=kx��y������ƽ��3����λ���Ⱥ�ǡ�þ���B��-3��0����y���ϵ�C�㣮��������y=-x2+bx+c��x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ���Ҿ�����C����Գ�����ֱ��BC���ڵ�E����x�ύ�ڵ�F��
��1����ֱ��BC�������ߵĽ���ʽ��
��2���������ߵĶ���ΪD����P�������ߵĶԳ����ϣ�����APD=��ACB�����P�����ꣻ
��3�������������Ƿ���ڵ�M��ʹ��ֱ��CM���ı���EFOC�ֳ������ȵ������֣������ڣ������ֱ��CM�Ľ���ʽ���������ڣ���˵�����ɣ�

��1����ֱ��BC�������ߵĽ���ʽ��
��2���������ߵĶ���ΪD����P�������ߵĶԳ����ϣ�����APD=��ACB�����P�����ꣻ
��3�������������Ƿ���ڵ�M��ʹ��ֱ��CM���ı���EFOC�ֳ������ȵ������֣������ڣ������ֱ��CM�Ľ���ʽ���������ڣ���˵�����ɣ�

��1����y=kx��y������ƽ��3����λ���Ⱥ�y���ϵĵ�C��
���ʱֱ�ߵĽ���ʽΪy=kx-3����x=0����y=-3��
��C��0��-3����
��ֱ��BC�Ľ���ʽΪy=kx-3��
��B��-3��0����ֱ��BC�ϣ�
��-3k-3=0���k=-1��
��ֱ��BC�Ľ���ʽΪy=-x-3��
��������y=-x2+bx+c����B��C��
��
��
���
��
�������ߵĽ���ʽΪy=-x2-4x-3��
��2����y=-x2-4x-3���ɵ�D��-2��1����A��-1��0����
��OB=3��OC=3��OA=1��AB=2��
�ɵá�OBC�ǵ���ֱ�������Σ�
���OBC=45�㣬CB=3
��
�������߶Գ�����x�ύ�ڵ�F��
��AF=
AB=1��
����AE��
�ߡ�AEF=��BEF=45�㣬
���AEB=90�㣮
�ɵ�BE=AE=
��CE=2
��
�ڡ�AEC���AFP�У���AEC=��AFP=90�㣬��ACE=��APF��
���AEC����AFP��
��
=
��
=
����ã�PF=2��
�ߵ�P�������ߵĶԳ����ϣ�
���P��������-2��-2������-2��2����
��3�����ڣ�
��D��-2��1����C��0��-3����ֱ��BC�Ľ���ʽΪy=-x-3��
��F��-2��0����E��-2��-1����
��S����EFOC=
��EF+OC��•OF=
����1+3����2=4��
�ߵ�ֱ��CM����Fʱ��S��OCF=
OC•OF=
��3��2=3��
S����EFOC=2��
��ֱ�߱ع��߶�OF����ֱ��CM���߶�OF����ڵ�G��x��0������S��OCG=
OC•OG=
��3��
��-x��=2�����x=-
��
��G��-
��0����
��ֱ��CM�Ľ���ʽΪy=kx+b��k��0����
��C��0��-3����G��-
��0����ֱ��CM�ϣ�
��
�����
��
��ֱ��CM�Ľ���ʽΪy=-
x-3��
���ʱֱ�ߵĽ���ʽΪy=kx-3����x=0����y=-3��
��C��0��-3����
��ֱ��BC�Ľ���ʽΪy=kx-3��
��B��-3��0����ֱ��BC�ϣ�
��-3k-3=0���k=-1��
��ֱ��BC�Ľ���ʽΪy=-x-3��
��������y=-x2+bx+c����B��C��
��
|
���
|
�������ߵĽ���ʽΪy=-x2-4x-3��
��2����y=-x2-4x-3���ɵ�D��-2��1����A��-1��0����
��OB=3��OC=3��OA=1��AB=2��
�ɵá�OBC�ǵ���ֱ�������Σ�
���OBC=45�㣬CB=3
| 2 |
�������߶Գ�����x�ύ�ڵ�F��
��AF=
| 1 |
| 2 |
����AE��
�ߡ�AEF=��BEF=45�㣬
���AEB=90�㣮
�ɵ�BE=AE=
| 2 |
| 2 |
�ڡ�AEC���AFP�У���AEC=��AFP=90�㣬��ACE=��APF��
���AEC����AFP��
��
| AE |
| AF |
| CE |
| PF |
| ||
| 1 |
2
| ||
| PF |
�ߵ�P�������ߵĶԳ����ϣ�
���P��������-2��-2������-2��2����
��3�����ڣ�
��D��-2��1����C��0��-3����ֱ��BC�Ľ���ʽΪy=-x-3��
��F��-2��0����E��-2��-1����
��S����EFOC=
| 1 |
| 2 |
| 1 |
| 2 |
�ߵ�ֱ��CM����Fʱ��S��OCF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��ֱ�߱ع��߶�OF����ֱ��CM���߶�OF����ڵ�G��x��0������S��OCG=
| 1 |
| 2 |
| 1 |
| 2 |
��-x��=2�����x=-
| 4 |
| 3 |
��G��-
| 4 |
| 3 |
��ֱ��CM�Ľ���ʽΪy=kx+b��k��0����
��C��0��-3����G��-
| 4 |
| 3 |
��
|
|
��ֱ��CM�Ľ���ʽΪy=-
| 9 |
| 4 |

��ϰ��ϵ�д�
�����Ŀ



 ��0��������ΪP��
��0��������ΪP��