题目内容
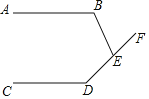
【题目】如图,AB∥CD,BE和DF相交于点E.
(1)若∠B=110°,∠D=145°,求∠BEF的度数;
(2)猜想∠B,∠D,∠BEF之间的关系,并说明理由.
【答案】(1)∠BEF=75°;(2)∠B﹣∠BEF+∠D=180°,见解析
【解析】
(1)过E作EG∥AB,依据AB∥CD,即可得到GE∥CD,依据平行线的性质,即可得到∠BED的度数,利用平角的定义即可求出∠BEF的度数;(2)过E作EG∥AB,依据AB∥CD,即可得到GE∥CD,依据平行线的性质,即可得到∠B+∠BED+∠D=360°,根据∠BEF=180°-∠BED即可得∠B﹣∠BEF+∠D=180°.
(1)如图,过E作EG∥AB,
∵AB∥CD,
∴GE∥CD,
∴∠B+∠BEG=180°,∠D+∠DEG=180°,
∵∠B=110°,∠D=145°,
∴∠BEG=70°,∠DEG=35°,
∴∠BED=∠BEG+∠DEG=105°,
∴∠BEF=180°﹣105°=75°;
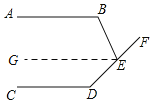
(2)∠B﹣∠BEF+∠D=180°.
如图,过E作EG∥AB,
∵AB∥CD,
∴GE∥CD,
∴∠B+∠BEG=180°,∠D+∠DEG=180°,
∴∠B+∠BED+∠D=360°,
又∵∠BED=180°﹣∠BEF,
∴∠B+180°﹣∠BEF+∠D=360°,
∴∠B﹣∠BEF+∠D=180°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目