题目内容
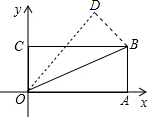如图，在直角坐标系中，将矩形OABC沿OB对折，使点A落在点D处，已知OA=2| 3 |
（
，3）
| 3 |
（
，3）
．| 3 |
分析：本题应先根据题意得出∠2和∠3的角度．再根据三角形全等得出∠1的度数，最后通过作出辅助线ED⊥y轴于点E，根据∠1的三角函数值即可得出D点的坐标．
解答：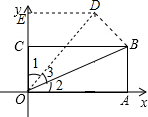
解：∵OA=2
，AB=2，
∴tan∠2=
=
=
，
∴∠2=30°，
由折叠方法可得∠3=∠2=30°，OD=0A=2
，
∵∠COA=90°，
∴∠1=30°，
作ED⊥y轴于点E，利用三角函数可得ED=
，EO=3，
故D的坐标为：（
，3），
故答案为：（
，3）．
解：∵OA=2| 3 |
∴tan∠2=
| AB |
| AO |
2
| ||
| 2 |
| 3 |
∴∠2=30°，
由折叠方法可得∠3=∠2=30°，OD=0A=2
| 3 |
∵∠COA=90°，
∴∠1=30°，
作ED⊥y轴于点E，利用三角函数可得ED=
| 3 |
故D的坐标为：（
| 3 |
故答案为：（
| 3 |
点评：此题主要考查了图形的折叠，以及三角函数定义，解决问题的关键是根据已知条件得到∠1和∠2的角度．
练习册系列答案
相关题目
如图，在直角坐标系中，点P的坐标为（3，4），将OP绕原点O逆时针旋转90°得到线段OP′．
，2）．画出△ABC的两个位似图形△A1B1C1，△A2B2C2，同时满足下列两个条件：