题目内容
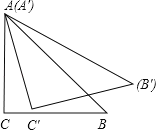
【题目】如图，将等腰直角△ABC绕底角顶点A逆时针旋转15°后得到△A′B′C′，如果AC＝
，那么两个三角形的重叠部分面积为_____．
【答案】
.
【解析】
根据等腰直角三角形的性质可得∠BAC=45°，根据旋转角可得∠CAC′=15°，然后求出∠C′AB=30°，旋转前后对应边相等，对应角相等，AC′=AC=
，∠C′=∠C=90°，解直角三角形，可求重叠部分面积．
解：∵等腰直角△ABC绕点A逆时针旋转15°后得到△AB′C′，
∴∠CAB=45°，∠CAC′＝15°，
∴∠C′AB＝∠CAB﹣∠CAC′＝45°﹣15°＝30°，
∵AC′＝AC＝，∠C′=∠C=90°，
∴重叠部分的面积＝
××tan30°×＝.
故答案为：．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
