题目内容
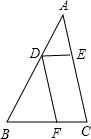已知△ABC，D是边AB上的一点，DE∥BC交AC于点E，DF∥AC交BC于点F，若△ADE、△DBF的面积分别为1和2，则四边形DECF的面积为
- A.3
- B.2
- C.2
- D.3
C
分析：解答本题只需画出示意图，先判断出△BFD∽△DEA，然后根据面积比等于相似比的平方得出△ABC的面积，进而根据SDECF=SABC-SADE-SDBF可得出答案．
解答：如图所示：
由题意得：△BFD∽△DEA，
∴可得：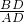
=
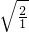=（面积比等于相似比的平方），
∴
=
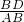，设SABC=y，
∴
=
，
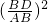∴可得y=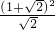
=2+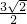
又∵△ADE、△DBF的面积分别为1和2，
∴SDECF=SABC-SADE-SDBF=2．
故选C．
点评：本题考查了面积及等积变换，难度适中，对于此类题目要先画出示意图，然后根据比例的性质得出要求图形的面积表达式，进而得出答案．
分析：解答本题只需画出示意图，先判断出△BFD∽△DEA，然后根据面积比等于相似比的平方得出△ABC的面积，进而根据SDECF=SABC-SADE-SDBF可得出答案．
解答：如图所示：
由题意得：△BFD∽△DEA，
∴可得：
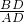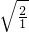==（面积比等于相似比的平方），∴
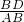=，设SABC=y，∴
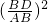=，∴可得y=
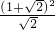=2+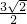又∵△ADE、△DBF的面积分别为1和2，
∴SDECF=SABC-SADE-SDBF=2
．故选C．
点评：本题考查了面积及等积变换，难度适中，对于此类题目要先画出示意图，然后根据比例的性质得出要求图形的面积表达式，进而得出答案．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知△ABC，P是边AB上的一点，连接CP，以下条件中不能确定△ACP与△ABC相似的是（ ）| A、∠ACP=∠B | ||||
| B、∠APC=∠ACB | ||||
| C、AC2=AP•AB | ||||
D、
|
已知△ABC，D是边AB上的一点，DE∥BC交AC于点E，DF∥AC交BC于点F，若△ADE、△DBF的面积分别为1和2，则四边形DECF的面积为（ ）
如图，已知△ABC，P是边AB上一点，连接CP，使△ACP∽△ABC成立的条件是（ ）
