题目内容
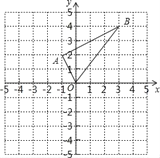
【题目】已知矩形0ABC在平面直角坐标系内的位置如图所示,点0为坐标原点,点A的坐标为(10,0),点B的坐标为(10,8),点Q为线段AC上-点,其坐标为(5,n).
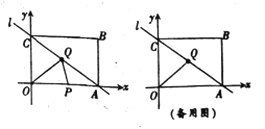
(1)求直线AC的表达式
(2)如图,若点P为坐标轴上-动点,动点P沿折线AO→0C的路径以每秒1个单位长度的速度运动,到达C处停止求Δ0PQ的面积S与点P的运动时间t(秒)的函数关系式.
(3)若点P为坐标平面内任意-.点,是否存在这样的点P,使以0,C,P,Q为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
【答案】(1) ![]() ; (2) 当点P在A0上运动时,S=2t+20 ,当点P在0C上运动时,S
; (2) 当点P在A0上运动时,S=2t+20 ,当点P在0C上运动时,S ![]() (10≤t≤18) ;(3)点P的坐标为(5,12),(5,-4),(-5,4)
(10≤t≤18) ;(3)点P的坐标为(5,12),(5,-4),(-5,4)
【解析】
(1)由矩形的性质可得出点C的坐标,根据点A,C的坐标,利用待定系数法可求出直线AC的解析式;
(2)利用一次函数图象上点的坐标特征可求出点Q的坐标,分点P在OA和点P在OC上两种情况,利用三角形的面积公式可找出S与t之间的函数关系式;
(3)分OC为对角线、OQ为对角线以及CQ为对角线三种情况,利用平行四边形的性质(对角线互相平分)即可求出点P的坐标.
解:(1)没直线AC的解析式为y=kx+b,
由题知C(0,8),A(10,0)
∴![]()
解之得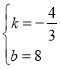
∴![]()
(2)∵Q(5,n)在直线![]() 上
上
∴n=4
∴Q(5,4)
当点P在A0上运动时,![]()
=2t+20
当点P在0C上运动时,
![]()
![]() (10≤t≤18)
(10≤t≤18)
(3) 设点P的坐标为(a,c),分三种情况考虑(如图2):
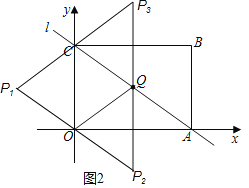
①当OC为对角线时,∵O(0,0),C(0,8),Q(5,4),
∴![]() ,解得:
,解得:![]() ,
,
∴点P1的坐标为(-5,4);
②当OQ为对角线时,∵O(0,0),C(0,8),Q(5,4),
∴![]() ,解得:
,解得:![]() ,
,
∴点P2的坐标为(5,-4);
③当CQ为对角线时,∵O(0,0),C(0,8),Q(5,4),
∴![]() ,解得:
,解得:![]() span>,
span>,
∴点P3的坐标为(5,12).
综上所述:存在点P,使以O,C,P,Q为顶点的四边形为平行四边形,点P的坐标为(-5,4),(5,-4),(5,12).
故答案为:(1) ![]() ; (2) 当点P在A0上运动时,S=2t+20 ,当点P在0C上运动时,S
; (2) 当点P在A0上运动时,S=2t+20 ,当点P在0C上运动时,S ![]() (10≤t≤18) ;(3)点P的坐标为(5,12),(5,-4),(-5,4) .
(10≤t≤18) ;(3)点P的坐标为(5,12),(5,-4),(-5,4) .

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】某童装厂现有甲种布料38米,乙种布料26米,现计划用这两种布料生产L.M两种型号的童装共50套.已知做一套L.M型号的童装所需用布料和所获得利润如下表:
甲种布料 | 乙种布料 | 获 利 | |
L型 | 0.5米 | 1米 | 45元 |
M型 | 0.9米 | 0.2米 | 30元 |
假设L型号的服装生产![]() 套,请你写出满足题意的不等式组,求出其解集;并根据计算结果,设计生产方案.
套,请你写出满足题意的不等式组,求出其解集;并根据计算结果,设计生产方案.