Question

【题目】在平面直角坐标系xoy中，直线l1:与x轴交于点A，与y轴交于点B，且点C的坐标为（4，-4）.

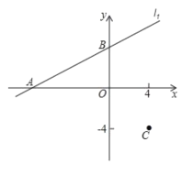
（1）点A的坐标为 ，点B的坐标为 ；（用含b的式子表示）

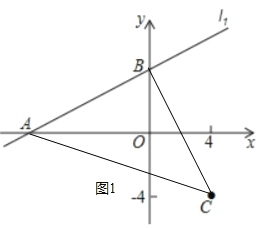
（2）当b=4时，如图所示，连接AC，BC，判断△ABC的形状，并证明你的结论.

Answer 1

【答案】（1）（-2b，0），（0，b）；（2）△ABC是等腰直角三角形，证明见详解.

【解析】

（1）根据待定系数法，令y=0，x=0即可解决问题；

（2）△ABC是等腰直角三角形，根据两点间距离公式以及勾股定理的逆定理即可判断；

解：（1）在中，

令x=0，则y=b，

∴点B的坐标为：（0，b）；

令y=0，则，

∴点A的坐标为：（-2b，0）；

故答案为：（-2b，0），（0，b）.

（2）△ABC是等腰直角三角形．

理由：∵b=4，

∴A（-8，0），B（0，4），

∵C（4，-4），

∴，，，

∴AB=AC，

∵，,

∴，

∴∠ABC=90°，

∴△ABC是等腰直角三角形．