ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=![]() +bx+cгыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ4ЃЌ0ЃЉСНЕуЃЌ
+bx+cгыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ4ЃЌ0ЃЉСНЕуЃЌ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЃЈ1ЃЉжаЕФХзЮяЯпНЛyжсгкCЕуЃЌдкИУХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУЁїQACЕФжмГЄзюаЁЃПШєДцдкЃЌЧѓГіQЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
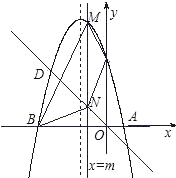
ЃЈ3ЃЉЩшДЫХзЮяЯпгыжБЯпy=ЉxдкЕкЖўЯѓЯоНЛгкЕуDЃЌЦНаагкyжсЕФжБЯпx=mЃЌ(![]() )гыХзЮяЯпНЛгкЕуMЃЌгыжБЯпy=ЉxНЛгкЕуNЃЌСЌНгBMЁЂCMЁЂNCЁЂNBЃЌЪЧЗёДцдкmЕФжЕЃЌЪЙЫФБпаЮBNCMЕФУцЛ§SзюДѓЃПШєДцдкЃЌЧыЧѓГіmЕФжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
)гыХзЮяЯпНЛгкЕуMЃЌгыжБЯпy=ЉxНЛгкЕуNЃЌСЌНгBMЁЂCMЁЂNCЁЂNBЃЌЪЧЗёДцдкmЕФжЕЃЌЪЙЫФБпаЮBNCMЕФУцЛ§SзюДѓЃПШєДцдкЃЌЧыЧѓГіmЕФжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉy=![]() Љ3x+4ЃЛ(2)ДцдкЃЌдкИУХзЮяЯпЕФЖдГЦжсЩЯДцдкЕуQЃЈЉ1.5ЃЌ2.5ЃЉЃЌЪЙЕУЁїQACЕФжмГЄзюаЁЃЛЃЈ3ЃЉДцдкЃЌm=-1.
Љ3x+4ЃЛ(2)ДцдкЃЌдкИУХзЮяЯпЕФЖдГЦжсЩЯДцдкЕуQЃЈЉ1.5ЃЌ2.5ЃЉЃЌЪЙЕУЁїQACЕФжмГЄзюаЁЃЛЃЈ3ЃЉДцдкЃЌm=-1.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉAЃЌBЕФзјБъДњШыХзЮяЯпy=![]() +bx+cШЗЖЈНтЮіЪНЃЎ
+bx+cШЗЖЈНтЮіЪНЃЎ
ЃЈ2ЃЉAЃЌBЙигкЖдГЦжсЖдГЦЃЌBCгыЖдГЦжсЕФНЛЕуОЭЪЧЕуQЃЎ
ЃЈ3ЃЉЫФБпаЮBNCMЕФУцЛ§ЕШгкЁїMNBЕФУцЛ§+ЁїMNCЕФУцЛ§ЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпХзЮяЯпy=![]() +bx+cгыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ4ЃЌ0ЃЉСНЕуЃЌ
+bx+cгыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ4ЃЌ0ЃЉСНЕуЃЌ
НЋAЁЂBСНЕузјБъДњШыХзЮяЯпЗНГЬЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЫљвдЃЌИУХзЮяЯпЕФНтЮіЪНЮЊЃКy=![]() Љ3x+4ЃЛ
Љ3x+4ЃЛ
ЃЈ2ЃЉДцдкЃЎРэгЩШчЯТЃК
ЁпгЩЧАУцЕФМЦЫуПЩвдЕУЕНЃЌCЃЈ0ЃЌ4ЃЉЃЌЧвХзЮяЯпЕФЖдГЦжсЮЊжБЯпx=Љ1.5ЃЌ
ЁргЩХзЮяЯпЕФЖдГЦадЃЌЕуAЁЂBЙигкжБЯпx=1ЖдГЦЃЌ
ЁрЕБQC+QAзюаЁЪБЃЌЁїQACЕФжмГЄОЭзюаЁЃЌ
ЖјЕБЕуQдкжБЯпBCЩЯЪБQC+QAзюаЁЃЌ
ДЫЪБжБЯпBCЕФНтЮіЪНЮЊy=x+4ЃЌ
ЕБx=Љ1.5ЪБЃЌy=2.5ЃЌ
ЁрдкИУХзЮяЯпЕФЖдГЦжсЩЯДцдкЕуQЃЈЉ1.5ЃЌ2.5ЃЉЃЌЪЙЕУЁїQACЕФжмГЄзюаЁЃЛ
ЃЈ3ЃЉгЩЬтвтЃЌMЃЈmЃЌ![]() Љ3m+4ЃЉЃЌNЃЈmЃЌЉmЃЉЃЌ
Љ3m+4ЃЉЃЌNЃЈmЃЌЉmЃЉЃЌ
ЁрЯпЖЮMN=![]() Љ3m+4ЉЃЈЉmЃЉ=
Љ3m+4ЉЃЈЉmЃЉ=![]() Љ2m+4=
Љ2m+4=![]() +5ЃЌ
+5ЃЌ
Ёп![]() =0.5MNЁСBO=2MN=
=0.5MNЁСBO=2MN=![]() +10ЃЌ
+10ЃЌ
ЁрЕБm=Љ1ЪБЃЈдк![]() ФкЃЉЃЌЫФБпаЮBNCMЕФУцЛ§SзюДѓЃЎ
ФкЃЉЃЌЫФБпаЮBNCMЕФУцЛ§SзюДѓЃЎ