题目内容
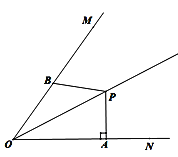
【题目】如图,P为∠MON平分线上一点,且OP=![]() ,PA⊥ON,垂足为A,B为射线OM上一动点,若AP=1,PB=
,PA⊥ON,垂足为A,B为射线OM上一动点,若AP=1,PB=![]() ,则OB=______.
,则OB=______.
【答案】2+![]() 或2-
或2- ![]()
【解析】过点P作PC⊥OM,然后分两种情况讨论:
如图1, 过点P作PC⊥OM,
因为P为∠MON平分线上一点,PA⊥ON,
所以PA=PC=1,
在Rt△OPC中,由勾股定理可得:
OC=![]() ,
,
在Rt△BPC中,由勾股定理可得:
BC=![]() ,
,
所以OB= OC-BC=2-![]() ,
,
如图2, 过点P作PC⊥OM,
因为P为∠MON平分线上一点,PA⊥ON,
所以PA=PC=1,
在Rt△OPC中,由勾股定理可得:
OC=![]() ,
,
在Rt△BPC中,由勾股定理可得:
BC=![]() ,
,
所以OB= OC+BC=2+![]() ,
,
故答案为: 2+![]() 或2-
或2-![]() .
.


点睛:本题主要考查角平分线的性质和勾股定理,解决本题关键是要分情况讨论进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目