题目内容
【题目】如图,已知AB∥CD,O为∠CAB,∠ACD的角平分线的交点,OE⊥AC于E,且OE=2,则两平行线间AB,CD的距离等于 . 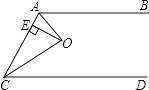
【答案】4
【解析】解:如图,过点O作MN,MN⊥AB于M,交CD于N, 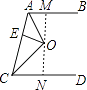
∵AB∥CD,
∴MN⊥CD,
∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=2,
∴OM=OE=2,
∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,
∴ON=OE=2,
∴MN=OM+ON=4,
即AB与CD之间的距离是4.
所以答案是:4.
【考点精析】根据题目的已知条件,利用平行线之间的距离和角平分线的性质定理的相关知识可以得到问题的答案,需要掌握两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目