题目内容
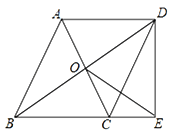
【题目】如图,在△ABC中,点D为∠ABC的平分线BD上一点,连接AD,过点D作EF∥BC交AB于点E,交AC于点F.
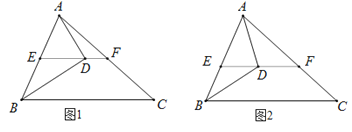
(1)如图1,若AD⊥BD于点D,∠BEF=130°,求∠BAD的度数;
(2)如图2,若∠ABC=α,∠BDA=β,求∠FAD+∠C的度数(用含α和β的代数式表示).
【答案】(1)65°;(2)∠FAD+∠C=β﹣![]() α.
α.
【解析】试题分析:(1)利用角平分线可得![]() 是等腰三角形,可以得到∠ABD的度数,AD⊥BD,所以可以得到∠BAD的度数.
是等腰三角形,可以得到∠ABD的度数,AD⊥BD,所以可以得到∠BAD的度数.
(2)利用(1)的方法,可求得∠FAD+∠C的度数.
试题解析:
解:(1)∵EF∥BC,∠BEF=130°,
∴∠EBC=50°,∠AEF=50°,
又∵BD平分∠EBC,
∴∠EBD=∠BDE=∠DBC=25°,
又∵∠BDA=90°,
∴∠EDA=65°,
∴∠BAD=65°.
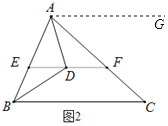
(2)如图2,过点A作AG∥BC,
则∠BDA=∠DBC+∠DAG=∠DBC+∠FAD+∠FAG=∠DBC+∠FAD+∠C=β,
则∠FAD+∠C=β﹣∠DBC=β﹣![]() ∠ABC=β﹣
∠ABC=β﹣![]() α.
α.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目