Question

【题目】如图，一次函数y1＝k1x+b（k1、b为常数，k1≠0）的图象与反比例函数y2＝（k2≠0）的图象交于点A（m，1）与点B（﹣1，﹣4）．

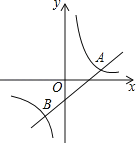
（1）求反比例函数与一次函数的解析式；

（2）根据图象说明，当x为何值时，k1x+b﹣＜0；

（3）若动点P是第一象限内双曲线上的点（不与点A重合），连接OP，过点P作y轴的平行线交直线AB于点C，连接OC，若△POC的面积为3，求点P的坐标．

Answer 1

【答案】（1）y1＝x﹣3；；（2）x＜﹣1或0＜x＜4；（3）点P的坐标为或（1，4）或（2，2）

【解析】

（1）把B点坐标代入反比例函数解析式可求得k2的值，把点A（m，1）代入求得的反比例函数的解析式求得m，然后利用待定系数法即可求得一次函数的解析式；

（2）直接由A、B的坐标根据图象可求得答案；

（3）设点P的坐标为，则C（m，m﹣3），由△POC的面积为3，得到△POC的面积，求得m的值，即可求得P点的坐标．

解：（1）将B（﹣1，﹣4）代入得：k2＝4

∴反比例函数的解析式为，

将点A（m，1）代入y2得，解得m＝4，

∴A（4，1）

将A（4，1）、B（﹣1，﹣4）代入一次函数y1＝k1x+b得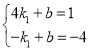

解得k1＝1，b＝﹣3

∴一次函数的解析式为y1＝x﹣3；

（2）由图象可知：x＜﹣1或0＜x＜4时，k1x+b﹣＜0；

（3）如图：设点P的坐标为，则C（m，m﹣3）

∴，点O到直线PC的距离为m

∴△POC的面积＝，

解得：m＝5或﹣2或1或2，

又∵m＞0

∴m＝5或1或2，

∴点P的坐标为或（1，4）或（2，2）．