Question

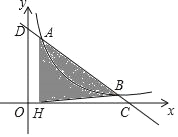
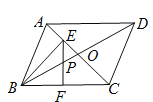
【题目】如图，在□ABCD中，对角线AC、BD相交于点O，AB=OB，E为AC上一点，BE平分∠ABO，EF⊥BC于点F，∠CAD=45°，EF交BD于点P，BP=，则BC的长为_______．

Answer 1

【答案】4

【解析】

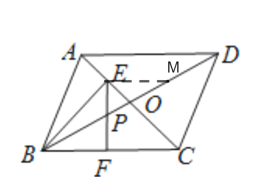
过点E作EM∥AD，由△ABO是等腰三角形，根据三线合一可知点E是AO的中点，可证得EM=AD=BC，根据已知可求得∠CEF=∠ECF=45°，从而得∠BEF=45°，△BEF为等腰直角三角形，可得BF=EF=FC=BC，因此可证明△BFP≌△MEP（AAS），则EP=FP=FC，在Rt△BFP中，利用勾股定理可求得x，即得答案．

过点E作EM∥AD，交BD于M，设EM=x，

∵AB=OB，BE平分∠ABO，

∴△ABO是等腰三角形，点E是AO的中点，BE⊥AO，∠BEO=90°，

∴EM是△AOD的中位线，

又∵ABCD是平行四边形，

∴BC=AD=2EM=2x，

∵EF⊥BC， ∠CAD=45°，AD∥BC，

∴∠BCA=∠CAD=45°，∠EFC=90°，

∴△EFC为等腰直角三角形，

∴EF=FC，∠FEC=45°，

∴∠BEF=90°-∠FEC=45°，

则△BEF为等腰直角三角形，

∴BF=EF=FC=BC=x，

∵EM∥BF，

∴∠EMP=∠FBP，∠PEM=∠PFB=90°，EM=BF，

则△BFP≌△MEP（ASA），

∴EP=FP=EF=FC=x，

∴在Rt△BFP中，，

即：，

解得：，

∴BC=2=4，

故答案为：4．