题目内容
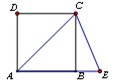
如图,四边形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,则AD与BC之间的距离等于 .

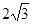
试题分析:首先过点D作DE∥AC交BC的延长线于点E,过点D作DF⊥BC于点F,易得四边形ACED是平行四边形,DE⊥BD,又由BC=5,AD=3,∠DBC=30°,即可求得BE,DE,BD的长,又由直角三角形的面积,即可得
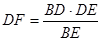 ,则可求得答案.
,则可求得答案.过点D作DE∥AC交BC的延长线于点E,过点D作DF⊥BC于点F,
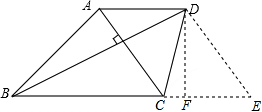
∵AD∥BC,
∴四边形ACED是平行四边形,
∴CE=AD=3,
∵AC⊥BD,
∴DE⊥BD,
∵BC=5,
∴BE=BC+CE=5+3=8,
∵∠DBC=30°,
∴DE=
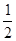 BE=4,
BE=4,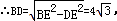
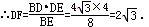
点评:此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 ,则下底BC的长为( )
,则下底BC的长为( )

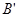 与点B关于AE对称,
与点B关于AE对称,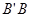 与AE交于点F,连接
与AE交于点F,连接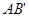 ,
,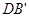 ,FC。下列结论:①
,FC。下列结论:①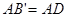 ;②
;②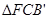 为等腰直角三角形;③
为等腰直角三角形;③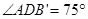 ;④
;④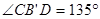 。其中正确的是( )
。其中正确的是( )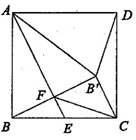





 ABCD的两条对角线线交于O,且
ABCD的两条对角线线交于O,且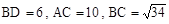 。
。
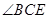 = .
= .