题目内容
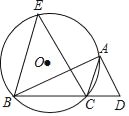
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连结EF,则线段EF长度的最小值为_____.

【答案】![]()
【解析】
由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,此时线段EF=2EH=2OEsin∠EOH=2OEsin60°,当半径OE最短时,EF最短,连接OE,OF,过O点作OH⊥EF,垂足为H,在Rt△ADB中,解直角三角形求直径AD,由圆周角定理可知∠EOH=![]() ∠EOF=∠BAC=60°,在Rt△EOH中,解直角三角形求EH,由垂径定理可知EF=2EH,即可求出答案.
∠EOF=∠BAC=60°,在Rt△EOH中,解直角三角形求EH,由垂径定理可知EF=2EH,即可求出答案.
由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,
如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
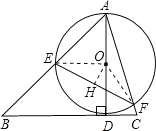
∵在Rt△ADB中,∠ABC=45°,AB=4,
∴AD=BD=2![]() ,即此时圆的直径为2
,即此时圆的直径为2![]() ,
,
由圆周角定理可知∠EOH=∠EOF=∠BAC=60°,
∴在Rt△EOH中,EH=OEsin∠EOH=![]() ,
,
由垂径定理可知EF=2EH=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目