题目内容
【题目】某兴趣小组想测量位于一池塘两端的A、B之间的距离，组长小明带领小组成员沿着与直线AB平行的道路EF行走，当行走到点C处，测得∠ACF=45°，再向前行走100米到达点D处，测得∠BDF=60°，已知AB与EF之间的距离为60米，求A、B两点的距离．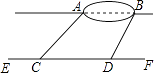
【答案】解：过点A作AG⊥EF于点G，过点B作BH⊥EF于点H，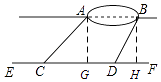
∵∠ACF=45°，
∴AG=CG=60，
∵∠BDF=60°，
∴tan60°= 
，
∴DH= 
，
∵CD=100，
∴DG=CD﹣CG=40，
∴GH=AB=DG+DH=40+20 
【解析】过点A作AG⊥EF于点G，过点B作BH⊥EF于点H，利用∠ACF=45°与∠BDF=60°即可求出CG与DH的长度，从而可求出AB的长度．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
【题目】虽然近几年无锡市政府加大了太湖水治污力度，但由于大规模、高强度的经济活动和日益增加的污染负荷，使部分太湖水域水质恶化，富营养化不断加剧．为了保护水资源，我市制定一套节水的管理措施，其中对居民生活用水收费作如下规定：
月用水量（吨） | 单价（元/吨） |
不大于10吨部分 | 1.5 |
大于10吨不大于m吨部分（20≤m≤50） | 2 |
大于m吨部分 | 3 |
（1）若某用户六月份用水量为18吨，求其应缴纳的水费；
（2）记该用户六月份用水量为x吨，缴纳水费为y元，试列出y关于x的函数关系式；
（3）若该用户六月份用水量为40吨，缴纳水费y元的取值范围为70≤y≤90，试求m的取值范围．
