题目内容
在直角坐标系中,点P(1,-1)一定在( )
| A、抛物线y=x2上 | ||
B、双曲线y=
| ||
| C、直线y=x上 | ||
| D、直线y=-x上 |
分析:分别根据各个函数的特点分析得到,或直接把点(1,-1)代入下列各个解析式,判断左右是否相等,若相等则点P就在函数图象上,反之则不在.
解答:解:A、不能确定,当x≥0时,点P(1,-1)不在抛物线y=x2上;
B、不能确定,当x≥0时,点P(1,-1)不在双曲线y=
上;
C、因为-1≠1,故点P(1,-1)一定不在直线y=x上;
D、正确,因为直线y=-x上的点互为相反数,且没有定义域.
故选D.
B、不能确定,当x≥0时,点P(1,-1)不在双曲线y=
| 1 |
| x |
C、因为-1≠1,故点P(1,-1)一定不在直线y=x上;
D、正确,因为直线y=-x上的点互为相反数,且没有定义域.
故选D.
点评:此题综合了一次函数、二次函数、反比例函数图象上点的坐标特点,是中学阶段的重点内容.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
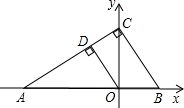 C作CB⊥AC,交x轴于B.
C作CB⊥AC,交x轴于B.