题目内容
如图，在直角坐标系中，点A的坐标为（-4，0），点C为y轴上一动点，连接AC，过点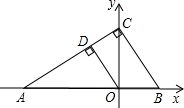
C作CB⊥AC，交x轴于B．（1）当点B坐标为（1，0）时，求点C的坐标；
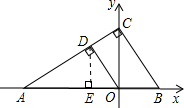
（2）如果sinA和cosA是关于x的一元二次方程x2+ax+b=0的两个实数根，过原点O作OD⊥AC，垂足为D，且点D的纵坐标为a2，求b的值．
分析：（1）在直角三角形AOC、BOC、ABC中，根据数量关系利用勾股定理可求出点C的坐标；
（2）先利用根与系数的关系确定a、b的数量关系，再利用三角函数和三角形的面积公式求出a2的值．
（2）先利用根与系数的关系确定a、b的数量关系，再利用三角函数和三角形的面积公式求出a2的值．
解答：解：（1）在Rt△AOC中，AO2+OC2=AC2，∴42+OC2=AC2． ①
在Rt△BOC中，BO2+OC2=BC2，∴12+OC2=BC2． ②
在Rt△ABC中，AC2+BC2=AB2，∴AC2+BC2=52． ③
由①、②两式可得AC2-BC2=15，
与第③式联立可解得BC=
，AC=2
．
∴OC=2．
∴点C的坐标为（0，2）．
（2）∵sinA和cosA是关于x的一元二次方程x2+ax+b=0的两个实数根，
∴sinA+cosA=-a，sinA•cosA=b．
又∵sinA2+cosA2=1，
则sinA2+cosA2=（sinA+cosA）2-2sinA•cosA=a2-2b=1．
∴a2=2b+1①，
在Rt△ADE中，sinA=
，
在Rt△AOD中，cosA=
，
∴sinA•cosA=
•
=
=
=b，
∴a2=4b②，
由①②，可得b=
．
在Rt△BOC中，BO2+OC2=BC2，∴12+OC2=BC2． ②
在Rt△ABC中，AC2+BC2=AB2，∴AC2+BC2=52． ③
由①、②两式可得AC2-BC2=15，
与第③式联立可解得BC=
| 5 |
| 5 |
∴OC=2．
∴点C的坐标为（0，2）．
（2）∵sinA和cosA是关于x的一元二次方程x2+ax+b=0的两个实数根，
∴sinA+cosA=-a，sinA•cosA=b．
又∵sinA2+cosA2=1，
则sinA2+cosA2=（sinA+cosA）2-2sinA•cosA=a2-2b=1．∴a2=2b+1①，
在Rt△ADE中，sinA=
| DE |
| AD |
在Rt△AOD中，cosA=
| AD |
| OA |
∴sinA•cosA=
| DE |
| AD |
| AD |
| OA |
| DE |
| OA |
| a2 |
| 4 |
∴a2=4b②，
由①②，可得b=
| 1 |
| 2 |
点评：此题综合考查了一元二次方程与解直角三角形的关系，难度较大．
练习册系列答案
相关题目
如图，在直角坐标系中，点P的坐标为（3，4），将OP绕原点O逆时针旋转90°得到线段OP′．
，2）．画出△ABC的两个位似图形△A1B1C1，△A2B2C2，同时满足下列两个条件：