题目内容
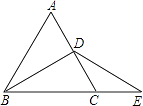
【题目】如图,在△ABC中,∠ABC=90°,∠A=30°,BC=4.若DE是△ABC的中位线,延长DE交∠ACM的平分线于点F,则DF的长为( ) 
A.6
B.7
C.8
D.9
【答案】A
【解析】解:∵∠ABC=90°,∠A=30°, ∴AC=2BC=8,∠ACB=60°,
∴CE= ![]() AC=4,
AC=4,
∵DE是△ABC的中位线,
∴DE= ![]() BC=2,DE∥BC,
BC=2,DE∥BC,
∵∠ACB=60°,
∴∠ACM=120°,
∵CF是∠ACM的平分线,
∴∠EFC=∠MCF=60°,
∵DE∥BC,
∴∠ECF=∠MCF=60°,
∴△ECF是等边三角形,
∴EF=EC=4,
∴DF=6,
故选:A.
【考点精析】利用含30度角的直角三角形和三角形中位线定理对题目进行判断即可得到答案,需要熟知在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.

【题目】某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人数) |
A | 80≤x<100 | 6 |
B | 100≤x<120 | 8 |
C | 120≤x<140 | m |
D | 140≤x<160 | 18 |
E | 160≤x<180 | 6 |

请结合图表解答下列问题:
(1)表中的m=;
(2)请把频数分布直方图补完整;
(3)这个样本数据的中位数落在第组;
(4)若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.
【题目】某大型文体活动需招募一批学生作为志愿者参与服务,已知报名的男生有420人,女生有400人,他们身高均在150≤x<175之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
组别 | 身高(cm) |
A | 150≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根据图表提供的信息,有下列几种说法
①估计报名者中男生身高的众数在D组;
②估计报名者中女生身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④估计身高在160cm至170cm(不含170cm)的学生约有400人
其中合理的说法是( )
A.①②
B.①④
C.②④
D.③④