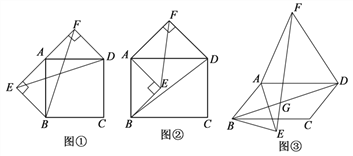
��Ŀ����
����Ŀ����ͼ������ABCD����ƽ��ֱ������ϵ�У�����AD����x����, ֱ��MN: y=x��8��x��ĸ�������ÿ��2����λ�ij���ƽ��,����ƽ�ƹ����и�ֱ�߱�����ABCD�ı߽صõ��߶γ���Ϊm,ƽ��ʱ��Ϊt, m��t�ĺ���ͼ����ͼ2��ʾ.

(1)��AB=6
�ٵ�A������Ϊ_____________,����ABCD�����Ϊ____________.
����a, b��ֵ;
(2)��AB=4����ƽ�ƹ�����,��ֱ��MNɨ������ABCD����� S�� t�ĺ�����ϵʽ,��д���Ա���t��ȡֵ��Χ.
���𰸡���1���٣�2��0����48����a=6![]() ��b=10����2��
��b=10����2�� .
.
��������
��1���������M������Ϊ��8��0��������ͼ2�ɵÿ�ʼƽ��3����M�����A������AM=6��OA=2��ƽ��7����M�����D������AD=![]() ���ɴ˿���õ�A������;���ABCD������������ͼ2������������λ�ã�ֱ��MN����B�͵�C��Ȼ��ͼ�Σ����ֱ��ƽ�Ƶ��ٶȣ��Ӷ����a��b��ֵ��
���ɴ˿���õ�A������;���ABCD������������ͼ2������������λ�ã�ֱ��MN����B�͵�C��Ȼ��ͼ�Σ����ֱ��ƽ�Ƶ��ٶȣ��Ӷ����a��b��ֵ��
��2���ɸ�����Ŀ�е�ͼ1��ͼ2��ƽ�Ʒ�Ϊ�ĸ��Σ�Ȼ������������ĸ�����ֱ��MN��x�ύ������꣬�ó�����ɨ�����ֵ�ͼ�Σ�Ȼ��ֱ����ɨ�����ֵ����.
�⣺��1���ٶ�ֱ��y=x��8����y=0����x��8=0����ã�x=8�����M������Ϊ��8��0����
����ͼ2�ɵÿ�ʼƽ��3����M�����A������AM=6��OA=2��ƽ��7����M�����D������AD=![]() ����A������Ϊ��2��0��������ABCD�����Ϊ6��8=48��
����A������Ϊ��2��0��������ABCD�����Ϊ6��8=48��
������ͼ1��ʾ����ֱ��MN������Bʱ��ֱ��MN��DA�ڵ�E��

�ߵ�A������Ϊ��2��0����AB=6�����B������Ϊ��2��6����
��ֱ��ME�Ľ���ʽΪy=x+c��
����B���������ã�2+c=6����c=4��
��ֱ��ME�Ľ���ʽΪy=x+4��
��y=0����ã�x+4=0�����x=��4��
���E����������4��0����
��BE=![]() ��
��
��a=6![]() ��
��
����ͼ2��ʾ����ֱ��MN������Cʱ��ֱ��MN��x���ڵ�F��

�ߵ�D������Ϊ����6��0�������C������Ϊ����6��6����
��MF�Ľ���ʽΪy=x+d��������6��6������ã���6+d=6�����d=12��
��ֱ��MF�Ľ���ʽΪy=x+12��
��y=0�����x+12=0�����x=��12��
���F����������12��0����
��b=7+6��2=10��
��2����������е�ͼ1��ͼ2���ɽ�ֱ��MN��ƽ�ư���ʱ���Ϊ�ĸ��Σ��ٴӳ�ʼλ��ƽ�Ƶ���A����ӣ���ֱ��MN��x��Ľ�����AE֮�ڣ���ֱ��MN��x��Ľ�����ED֮�ڣ���ֱ��MN��x��Ľ�����DG֮�ڣ�������G������ͼ��ʾ.

��0��t��3ʱ��ֱ��MN���ڽ٣���ʱֱ��MN�����ABCDû�н��㣬����S=0��
��3<t<5ʱ��ֱ��MN���ڽڣ���ʱֱ��MNɨ������ABCD�IJ���Ϊһ��С����ֱ�������Σ����������ε�����Ϊ2t��6���������Ϊ![]() ��
��
��5��t��7ʱ��ֱ��MN���ڽۣ���ʱֱ��MNɨ������ABCD�IJ���Ϊһ��ֱ�����Σ��ϵ�Ϊ2t��10���µ�Ϊ2t��6����Ϊ4���������Ϊ![]() ��
��
��7��t��9ʱ��ֱ��MN���ڽܣ���ʱֱ��MNɨ������ABCD�IJ���Ϊ����ABCD��ȥ���Ͻǵ�С����ֱ�������Σ�����AD=BC=8������������Ϊ8����2t��10��=18��2t���������Ϊ![]() .
.
����������S��t�ĺ�����ϵʽΪ .
.