Question

【题目】坐标平面内有4个点A(0,2),B(-2,0),C(1,-1),D(3,1).

(1)建立坐标系,描出这4个点;

(2)顺次连接A,B,C,D,组成四边形ABCD,求四边形ABCD的面积.

(3)线段AB,CD有什么关系?请说明理由.

Answer 1

【答案】(1)见解析；（2）8；（3）AB∥CD，理由见解析.

【解析】

（1）根据平面直角坐标系找出点A、B、C、D的位置，然后描出即可；（2）利用四边形ABCD所在的矩形的面积减去四周四个直角三角形的面积列式计算即可得解；

解： (1) 描点如下：

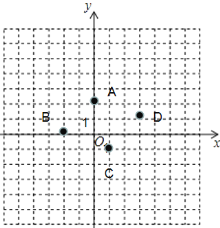
(2)四边形ABCD的面积为8.

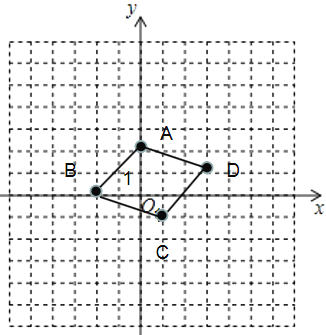
S四边形ABCD=5×3-×2×2-×3×1-×2×2-×3×1=8.

(3)AB∥CD, ,因为点A向右平移3个单位后,再向下平移1个单位,得到点D,而B点也是向右平移3个单位后,再向下平移1个单位,得到点C,所以AB∥CD.