题目内容
【题目】如图,是一个半圆和抛物线的一部分围成的“芒果”,已知点A、B、C、D分别是“芒果”与坐标轴的交点,AB是半圆的直径,抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() ,则图中CD的长为 .
,则图中CD的长为 . 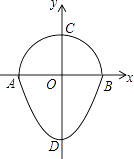
【答案】![]()
【解析】解:令y= ![]() x2﹣
x2﹣ ![]() =0,
=0,
解得x=1或﹣1,
即AB=2,
故CO=1,
令x=0,解得y=﹣ ![]() ,
,
即OD= ![]() ,
,
所以CD=CO+OD=1+ ![]() =
= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】利用抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
【题目】某班全体同学在“献爱心”活动中都捐了图书,捐书的情况如下表:
每人捐书的册数 | 5 | 10 | 15 | 20 |
相应的捐书人数 | 17 | 22 | 4 | 2 |
根据题目中所给的条件回答下列问题:
![]() 该班的学生共多少名?
该班的学生共多少名?
![]() 全班一共捐了多少册书?
全班一共捐了多少册书?
![]() 若该班所捐图书拟按图所示比例分,则给山区学校的书比送给本市兄弟学校的书多多少册?
若该班所捐图书拟按图所示比例分,则给山区学校的书比送给本市兄弟学校的书多多少册?





