��Ŀ����
��Rt��ABC����C=90�㣬DΪAB����һ�㣬��M��N�ֱ���BC��AC���ϣ���DM��DN����MF��AB�ڵ�F��NE��AB�ڵ�E��
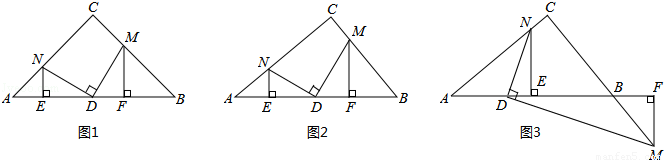
��1��������֤����ͼ1����AC=BC����DΪAB�е㣬��֤��DM=DN��AE=DF��
��2����չ̽������AC��BC��
����ͼ2����DΪAB�е㣬��1���е�����������һ���Գ�������ָ��������֤����
����ͼ3����BD=kAD�������С���M��BC���ϡ���Ϊ����M���߶�CB���ӳ����ϡ��������������䣬��̽��AE��DF��������ϵ������֤����
�⣺��1��֤������AC=BC�����ABCΪ����ֱ�������Σ�
��ͼ������OD����CD��AB��

�֡�DM��DN�����1=��2��
�ڡ�AND���CDM�У� ��
��
���AND�ա�CDM��ASA������DM=DN��
�ߡ�4+��1=90�㣬��1+��3=90�㣬���4=��3��
�ߡ�1+��3=90�㣬��3+��5=90�㣬���1=��5��
�ڡ�NED���DFM�У� ��
��
���NED�ա�DFM��ASA������NE=DF��
�ߡ�ANEΪ����ֱ�������Σ���AE=NE����AE=DF��
��2���ٴ�AE=DF��֤�����£�
�ɣ�1��֤����֪����DEN�ס�MFD���� ����MF•EN=DE•DF��
����MF•EN=DE•DF��
ͬ����AEN�ס�MFB����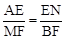 ����MF•EN=AE•BF��
����MF•EN=AE•BF��
��DE•DF=AE•BF���ࣨAD��AE��•DF=AE•��BD��DF����
��AD•DF=AE•BD����AE=DF��
�ڴ�DF=kAE��֤�����£�
�ɢ�ͬ���ɵã�DE•DF=AE•BF��
�ࣨAE��AD��•DF=AE•��DF��BD������AD•DF=AE•BD��
��BD=kAD����DF=kAE��
��������
�����������1����ͼ������CD��֤����AND�ա�CDM���ɵ�DM=DN��֤����NED�ա�DFM���ɵ�DF=NE���Ӷ��õ�AE=NE=DF��
��2������DΪAB�е㣬��ֱ�֤����DEN�ס�MFD����AEN�ס�MFB�����߶α�����ϵ����֤��AE=DF������Ȼ������
����BD=kAD��֤��˼·������ơ�

 23����ͼ����Rt��ABC�У���ACB=90�㣬D��E�DZ�AB�����㣬��CE����ֱ�ߴ�ֱƽ���߶�AD��CDƽ�֡�BCE��AC=5cm����BD�ij���
23����ͼ����Rt��ABC�У���ACB=90�㣬D��E�DZ�AB�����㣬��CE����ֱ�ߴ�ֱƽ���߶�AD��CDƽ�֡�BCE��AC=5cm����BD�ij���