题目内容
【题目】一个大正方形和四个全等的小正方形按图①、②两种方式摆放,设小正方形的边长为x,请仔细观察图形回答下列问题.
(1)用含a、b的代数式表示x,则x=____.
(2)用含a、b的代数式表示大正方形的边长____.(请将结果化为最简)
(3)利用前两问的结论求出图②的大正方形中未被小正方形覆盖部分的面积.(用a、b的代数式表示)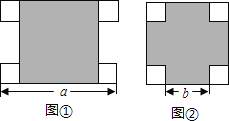
【答案】(1)![]() ;(2)
;(2)![]() ;(3)ab.
;(3)ab.
【解析】
(1)由大正方形的边长不变,可得出关于x的一元一次方程,解之即可得出x的值(用含a、b的代数式表示);
(2)将x的值代入a-2x,即可求出大正方形的边长;
(3)利用大正方形的面积-4×小正方形的面积,即可求出图②的大正方形中未被小正方形覆盖部分的面积.
(1)a-2x=b+2x,
∴x=![]() .
.
故答案为:![]() .
.
(2)大正方形的边长为a-2x=a-2×![]() =
=![]() .
.
故答案为:![]() .
.
(3)S=(![]() )2-4x2=(
)2-4x2=(![]() )2-4×(
)2-4×(![]() )2=ab.
)2=ab.

练习册系列答案
相关题目
【题目】某运输部门规定:办理托运,当一件物品的重量不超过![]() 千克时,需付基础费
千克时,需付基础费![]() 元和保险费
元和保险费![]() 元;为了限制过重物品的托运,当一件物品的重量超过
元;为了限制过重物品的托运,当一件物品的重量超过![]() 千克时,除了付以上基础费和保险费外,超过部分每千克还需付
千克时,除了付以上基础费和保险费外,超过部分每千克还需付![]() 元的超重费.设某件物品的重量为
元的超重费.设某件物品的重量为![]() 千克,支付费用为
千克,支付费用为![]() 元.
元.
(1)当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
(2)甲、乙、丙三人各托运一件物品,物品的重量与支付费用如下表所示:
托运人 | 物品重量/千克 | 支付费用/元 |
甲 | 14 | 33 |
乙 | 20 | 39 |
丙 | 30 |
|
根据以上提供的信息确定![]() 的值,并计算出丙所支付的费用
的值,并计算出丙所支付的费用![]() .
.