题目内容
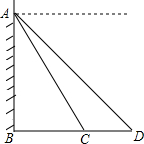
大楼AD的高为10米,不远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D点测得塔顶B点的仰角为30°,求塔BC的高度.


过点B作BE⊥AD,交AD延长线于点E.(1分)
在Rt△BED中,∵D点测得塔顶B点的仰角为30°,
∴∠BDE=60度.
设DE=x,则BE=
x.(2分)
在Rt△BEA中,∠BAE=30度,BE=
x.
∴AE=3x.(3分)
∴AD=AE-DE=3x-x=2x=10.
∴x=5.(4分)
∴BC=AD+DE=10+5=15(米).(5分)
答:塔BC的高度为15米.
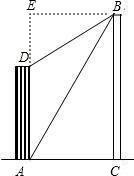
在Rt△BED中,∵D点测得塔顶B点的仰角为30°,
∴∠BDE=60度.
设DE=x,则BE=
| 3 |
在Rt△BEA中,∠BAE=30度,BE=
| 3 |
∴AE=3x.(3分)
∴AD=AE-DE=3x-x=2x=10.
∴x=5.(4分)
∴BC=AD+DE=10+5=15(米).(5分)
答:塔BC的高度为15米.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
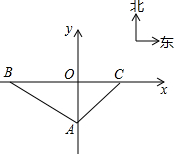 偏东45°方向上,另外一条高等级公路在y轴上,OA为其中一段.
偏东45°方向上,另外一条高等级公路在y轴上,OA为其中一段.
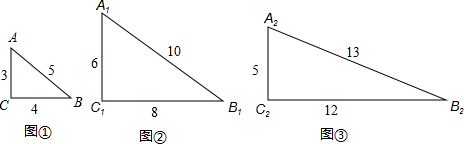
 为60米,山坡AC的坡度i=1:1.(提示:坡面的铅直高度与水平宽度的比称为坡度)
为60米,山坡AC的坡度i=1:1.(提示:坡面的铅直高度与水平宽度的比称为坡度)
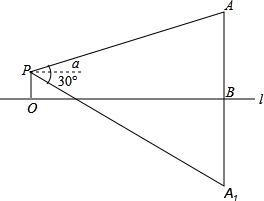
 处的俯角∠A=18°,2分钟后在B处观测到飞机正前方地面O处的俯角∠CBO=45°,求飞机的飞行高度.(精确到1米)
处的俯角∠A=18°,2分钟后在B处观测到飞机正前方地面O处的俯角∠CBO=45°,求飞机的飞行高度.(精确到1米)