题目内容
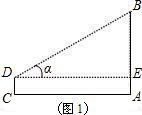
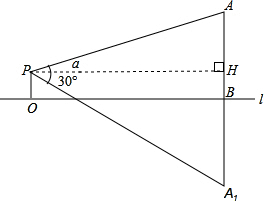
在湖心有一座小塔,小明想知道这座塔的高度,于是他在岸边架起了测角仪.他测量得数据如下(如图示):测角仪位置(P)距水平面(l)的距离为1.5米(即OP),测得塔顶A的仰角为α(其中tanα=
),测得塔顶在水中倒影A1(即AB=A1B)的俯角为30°.请你根据上述数据求出这座塔的高度(即AB).

| 1 |
| 3 |

作PH⊥AB交AB于点H.
由题意可知:四边形OPBH为矩形,
∴HB=OP=1.5.
在Rt△APH中,tanα=
,
令AH=k,PH=3k.
在Rt△A1PH中,∠A1PH=30°,
∴A1H=PH•tan30°=
k,
又AB=A1B,得:k+1.5=
k-1.5,
解得:k=
,
∴AB=AH+HB=3+
(米).
答:这座塔的高度是(3+
)米.
由题意可知:四边形OPBH为矩形,
∴HB=OP=1.5.
在Rt△APH中,tanα=
| 1 |
| 3 |
令AH=k,PH=3k.
在Rt△A1PH中,∠A1PH=30°,
∴A1H=PH•tan30°=
| 3 |
又AB=A1B,得:k+1.5=
| 3 |
解得:k=
3+3
| ||
| 2 |
∴AB=AH+HB=3+
3
| ||
| 2 |
答:这座塔的高度是(3+
3
| ||
| 2 |


练习册系列答案
相关题目