题目内容
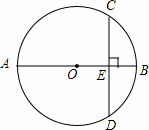
如图，A、B为⊙O上的两个定点，P是⊙O上的动点（P不与A、B重合），我们称∠APB是⊙O上关于A、B的滑动角．若⊙O的半径是1，
，则∠APB的取值范围为___________．
，则∠APB的取值范围为___________．45°≤∠APB≤60°或120°≤∠APB≤135°．
试题分析：连结AO并延长交⊙O于M，连接AB，BM，在劣弧AB上取一点N，连结AN，BN，则∠P=∠M，∠P+∠N=180°，∵AM为直径，∴∠ABM=90°，∵⊙O的半径是1，∴AM=2，在Rt△AMB中，sin∠M=
，∴2 sin∠M=AB，∵，∴
≤2 sin∠M ≤，∴
≤sin∠M ≤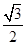
，∴45°≤∠M≤60°，即45°≤∠APB≤60°，∵∠M+∠N=180°，120°≤∠N≤135°，即120°≤∠APB≤135°，∴45°≤∠APB≤60°或120°≤∠APB≤135°．
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
