题目内容
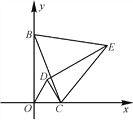
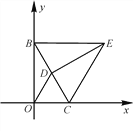
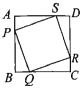
【题目】如图,![]() 四个小球分别从正方形的四个顶点
四个小球分别从正方形的四个顶点![]() 处出发(小球的大小忽略不计),以同样的速度分别沿
处出发(小球的大小忽略不计),以同样的速度分别沿![]() 方向滚动,其终点分别是点
方向滚动,其终点分别是点![]() ,顺次连接四个小球所在的位置,得到四边形
,顺次连接四个小球所在的位置,得到四边形![]() .
.
(1)不论小球滚动多长时间,求证;四边形![]() 总是正方形;
总是正方形;
(2)这个四边形在什么时候面积最大?
(3)在什么时侯四边形![]() 的面积为正方形
的面积为正方形![]() 面积的一半?请说明理由.
面积的一半?请说明理由.
【答案】(1)证明见解析;(2)当![]() 在即将出发或到达终点时面积最大,此时
在即将出发或到达终点时面积最大,此时![]() ;(3)当
;(3)当![]() 分别在
分别在![]() 的中点时,四边形
的中点时,四边形![]() 的面积为正方形
的面积为正方形![]() 面积的一半,理由见解析.
面积的一半,理由见解析.
【解析】
(1)根据题意得![]() ,再结合四边形
,再结合四边形![]() 是正方形,证明
是正方形,证明![]() ,即可证得四边形
,即可证得四边形![]() 为正方形;
为正方形;
(2) 根据题意得当![]() 在即将出发或到达终点时面积最大;
在即将出发或到达终点时面积最大;
(3) 当![]() 分别在
分别在![]() 的中点时,四边形
的中点时,四边形![]() 的面积为正方形
的面积为正方形![]() 面积的一半.
面积的一半.
解:(1)根据题意得![]() .
.
∵四边形![]() 是正方形,
是正方形,
∴![]() °,
°,
∴![]() .
.
∵在![]() 和
和![]() 中,
中,
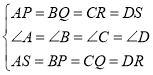 ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 为菱形,
为菱形,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 为正方形.
为正方形.
(2)根据题意得当![]() 在即将出发或到达终点时面积最大,此时
在即将出发或到达终点时面积最大,此时![]() .
.
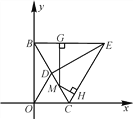
(3)当![]() 分别在
分别在![]() 的中点时,四边形
的中点时,四边形![]() 的面积为正方形
的面积为正方形![]() 面积的一半.
面积的一半.
理由如下:
设正方形![]() 的边长为
的边长为![]() ,
,
则根据题意知![]() .
.
在![]() 中,
中,![]() .
.
由勾股定理,得![]() ,
,
即![]() ,解得
,解得![]() ,
,
同理可得![]() .
.
∴当![]() 四个小球分别在正方形
四个小球分别在正方形![]() 各边的中点时,四边形
各边的中点时,四边形![]() 的面积为正方形
的面积为正方形![]() 面积的一半.
面积的一半.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】已知抛物线![]()
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线 | A(____) | B(____) | (1,0) | (0,-3) |
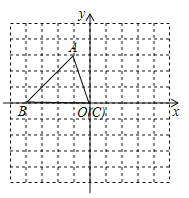
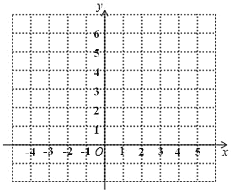
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中,画出抛物线![]()
(2)结合图象回答
①当x的取值范围为________时,y随x的增大而增大;
②当x________时,![]() ;
;
③当![]() 时,y的取值范围________.
时,y的取值范围________.