题目内容
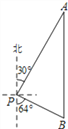
【题目】如图,某公安海上缉私局发现在我国领海的P处有一条走私船正以22海里/时的速度沿南偏东64的方向向公海逃窜,于是缉私局命令位于点P北偏东30方向A处的我公安缉私快艇前往拦截,已知P、A相距20海里,公安缉私快艇向正南方向行进计划在B处拦截走私船。
(1)求A、B两处的距离;(结果保留整数)
(2)若公安缉私快艇要在B处成功拦截走私船,则缉私快艇的速度至少为多少海里/时?
【参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2,![]() ,
,![]() ,
,![]() 】
】
【答案】(1) 22 海里;(2) 至少为44海里/小时.
【解析】分析:(1)过P点作PC⊥AB于点C,首先在RT△APC中,求得AC的长,然后在直角△BCP中,求得BC的长,再根据AB=AC+BC计算即可;(2)首先求得PB的距离,根据走私船的速度,求出时间,然后再根据AB=22, 设缉私快艇的速度为v,可求出缉私快艇的时间,两者比较,从而求解.
详解:(1)过P点作PC⊥AB于点C
Rt△APC中,∵ ∠A=30°,PA=20
∴ AC=![]() ,PC=10,
,PC=10,
Rt△PBC中,∵∠B=64°
∴ tan64°=![]() =2 PC=5
=2 PC=5
∴ AB=![]() +5 ≈22 海里 .
+5 ≈22 海里 .
(2)Rt△PBC中,∵BC=5,PC=10
∴PB=![]()
设走私船到B点时间为t,则t=![]()
设公安缉私船速度为V,则由题意 ![]() 解得 V≥44
解得 V≥44
答:缉私船的速度至少为44海里/小时才能在B拦截走私船。

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目