题目内容
【题目】定理描述
（1）如图1，用文字语言或符号语言叙述三角形中位线性质定理的内容．
．
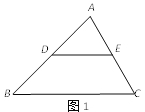
证法回顾
证明三角形中位线性质定理的方法很多，但多数都需要通过添加辅助线构图去完成．下列是其中一种证法的添加辅助线方法：
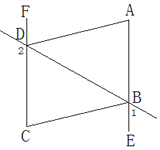
添加辅助线，如图2，在△ABC中，过点C作CF∥AB，与DE的延长线交于点F．
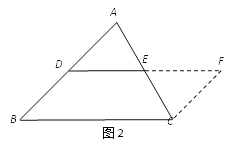
（2）上述证法中，证明三角形中位线定理中的DE∥BC的依据是（ ）
A．同位角相等，两直线平行．
B．平行四边形对边平行．
C．同旁内角互补，两直线平行．
D．平行于同一条直线的两条直线互相平行
拓展延伸
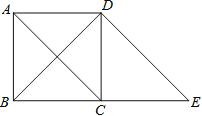
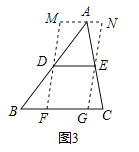
（3）利用证明三角形中位线定理获得的经验解决下面的问题：
如图3，在△ABC中，∠B=45°，AB=10，BC=8，DE是△ABC的中位线，过点D、E作DF∥EG，分别交BC于F、G，过点A作MN∥BC，分别与FD、GE的延长线交于M、N，则四边形MFGN周长的最小值是
【答案】（1）见解析；（2）B；（3）见解析.
【解析】
（1）分别运用文字语言和符号语言表述即可；
（2）作出图形，然后写出已知、求证，延长DE到F，使DE=EF，利用“边角边”证明△ADE和△CEF全等，根据全等三角形对应边相等可得AD=CF，全等三角形对应角相等可得∠F=∠ADE，再求出BD=CF，根据内错角相等，两直线平行判断出AB∥CF，然后判断出四边形BCFD是平行四边形，根据平行四边形的性质可得DF∥BC，DF=BC；
（3）先判断出四边形MFGN是平行四边形，再判断出MN=FG=DE=4，进而判断出MF⊥BC时，四边形MFGN的周长最小，最后构造出直角三角形求出AH即可得出结论．
（1）文字语言：三角形的中位线平行于第三边，并且等于第三边的一半；
符号语言：∵DE是△ABC的中位线，∴DE＝
BC， DE∥BC
（2）已知：△ABC中，点D、E分别是AB、AC的中点，
求证：DE=BC，DE∥BC，
证明：如图，延长DE到F，使DE=EF，连接CF，
∵点E是AC的中点，
∴AE=CE，
在△ADE和△CEF中，
，
∴△ADE≌△CEF（SAS），
∴AD=CF，∠ADE=∠F，
∴AB∥CF，
∵点D是AB的中点，
∴AD=BD，
∴BD=CF，
∴BD∥CF，
∴四边形BCFD是平行四边形，
∴DF∥BC，DF=BC，
∴DE∥BC且DE=BC．
故答案为：B．
（3）如图，
∵MN∥BC，FM∥GN，
∴四边形MFGN是平行四边形，
∴MF=NG，MN=FG，
∵DE是△ABC的中位线，
∴DE=BC=4，DE∥BC，
∴MN=FG=BC=4，
∴四边形MFGN周长=2（MF+FG）=2MF+8，
∴MF⊥BC时，MF最短，
即：四边形MFGN的周长最小，
过点A作AH⊥BC于H，
∴FM=AH
在Rt△ABH中，∠B=45°，AB=10，
∴AH=
=5
，
∴四边形MFGN的周长最小为2MF+8=10+8．
故答案为10+8．
