题目内容
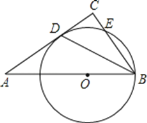
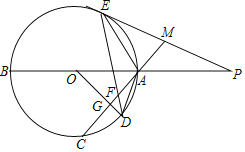
【题目】如图,已知AB是⊙O的直径,AC是弦(不是直径),OD⊥AC垂足为G交⊙O于D,E为⊙O上一点(异于A、B),连接ED交AC于点F,过点E的直线交BA、CA的延长线分别于点P、M,且ME=MF.
(1)求证:PE是⊙O的切线.
(2)若DF=2,EF=8,求AD的长.
(3)若PE=6![]() ,sin∠P=
,sin∠P=![]() ,求AE的长.
,求AE的长.
【答案】(1)详见解析;(2)![]() ;(3)2
;(3)2![]() .
.
【解析】
(1)连接OE,根据余角的性质和等腰三角形的性质得到∠D=∠OED,求得OE⊥PE,于是得到结论;
(2)根据垂径定理得到![]() ,求得∠FAD=∠AED,根据相似三角形的性质得到结论;
,求得∠FAD=∠AED,根据相似三角形的性质得到结论;
(3)设OE=x,解直角三角形即可得到结论.
(1)证明:连接OE,
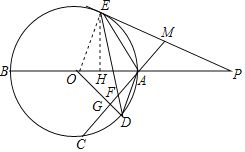
∵OD⊥AC,
∴∠DGF=90°,
∴∠D+∠DFG=∠D+∠AFE=90°,
∴∠DFG=∠AFE,
∵ME=MF,
∴∠MEF=∠MFE,
∵OE=OD,
∴∠D=∠OED,
∴∠OED+∠MEF=90°,
∴OE⊥PE,
∴PE是⊙O的切线;
(2)∵OD⊥AC,
∴![]() ,
,
∴∠FAD=∠AED,
∵∠ADF=∠EDA,
∴△DFA~△DAE,
∴![]() ,
,
∴AD2=DFDE=2×10=20,
∴AD=2![]() ;
;
(3)解:设OE=x,
∵sin∠P=![]() ,
,
∴OP=3x,
∴x2+(6![]() )2=(3x)2,
)2=(3x)2,
解得:x=3,
过E作EH垂直AB于H,
sin∠P=![]() ,
,
∴EH=2![]() ,
,
∵OH2+EH2=OE2,
∴OH=1,∴AH=2,
∵AE2=HE2+AH2,
∴AE=2![]() .
.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目