题目内容
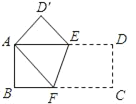
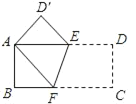
【题目】如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A、C重合,若其长BC为8,宽AB为4.
(1)求证:△AEF是等腰三角形.
(2)EF= .
【答案】(1)详见解析;(2)![]()
【解析】
(1)由矩形的性质以及翻折的性质证明∠AEF=∠AFE即可;
(2)设AF=AE=FC=x,在Rt△ABF中,利用勾股定理求出x,作FH⊥AE于H,在Rt△AHF中,利用勾股定理求出AH长,继而求出HE的长,然后在Rt△EFH中,利用勾股定理即可求得EF的长.
(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEF=∠EFC,
由翻折不变性可知:∠AFE=∠EFC,
∴∠AEF=∠AFE,
∴AE=AF,
∴△AEF是等腰三角形.
(2)设AF=AE=FC=x,
在Rt△ABF中,∵AF2=AB2+BF2,
∴x2=42+(8﹣x)2,
∴x=5,
作FH⊥AE于H.
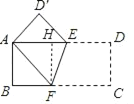
在Rt△AHF中,AH=![]() =3,
=3,
∴HE=AE﹣AH=2,
在Rt△EFH中,EF=![]() =
=![]() ,
,
故答案为:![]() .
.

【题目】某单位招聘员工两名,采取笔试与面试相结合的方式进行,两项成绩原始分满分均为100分,前六名选手的得分如下:
序号项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩(分) | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩(分) | 90 | 83 | 82 | 90 | 80 | 85 |
(1)这6名选手笔试成绩的中位数是________分,众数是________分.
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)在(2)的情况下________,(填序号)选手会被录取.
【题目】已知一水池的容积V(公升)与注入水的时间t(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
注入水的时间t(分钟) | 0 | 10 | … | 25 |
水池的容积V(公升) | 100 | 300 | … | 600 |
(1)求这段时间时V关于t的函数关系式(不需要写出函数的定义域);
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.