题目内容
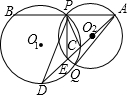 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且| PC |
| PD |
| CE |
| DE |
(1)∠CPE=∠DPE;
(2)AQ2-AP2=PC•PD.
分析:(1)过D作DM∥PE交CP的延长线于M,根据平行线分线段成比例定理求出PM=PD,推出∠M=∠PDM,根据平行线的性质得出∠M=∠CPE,∠DPE=∠PDM,即可得出答案;
(2)根据切割线定理得出AQ2=AP×AB,证△APC∽△DPB,推出
=
,得出AP×BP=PC×PD,代入即可得出答案.
(2)根据切割线定理得出AQ2=AP×AB,证△APC∽△DPB,推出
| AP |
| PD |
| PC |
| BP |
解答:(1)证明: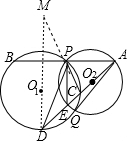 过D作DM∥PE交CP的延长线于M,
过D作DM∥PE交CP的延长线于M,
则
=
,
∵
=
,
∴PM=PD,
∴∠M=∠PDM,
∵PE∥MD,
∴∠M=∠CPE,∠DPE=∠PDM,
∴∠CPE=∠DPE;
(2)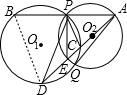 证明:连接BD,
证明:连接BD,
∵O2在AE上,
∴∠APE=∠BPE=90°,
∵∠CPE=∠DPE,
∴∠APC=∠BPD,
∵P、B、D、C四点共圆,
∴∠ACP=∠B,
∴△APC∽△DPB,
∴
=
,
∴AP×BP=PC×PD,
∵AQ切⊙O1于Q,APB是⊙O1的割线,
∴AQ2=AP×AB,
∴AQ2-AP2=AP×AB-AP2=AP(AB-AP)=AP×BP=PC•PD,
即AQ2-AP2=PC•PD.
 过D作DM∥PE交CP的延长线于M,
过D作DM∥PE交CP的延长线于M,则
| PC |
| PM |
| CE |
| DE |
∵
| PC |
| PD |
| CE |
| DE |
∴PM=PD,
∴∠M=∠PDM,
∵PE∥MD,
∴∠M=∠CPE,∠DPE=∠PDM,
∴∠CPE=∠DPE;
(2)
 证明:连接BD,
证明:连接BD,∵O2在AE上,
∴∠APE=∠BPE=90°,
∵∠CPE=∠DPE,
∴∠APC=∠BPD,
∵P、B、D、C四点共圆,
∴∠ACP=∠B,
∴△APC∽△DPB,
∴
| AP |
| PD |
| PC |
| BP |
∴AP×BP=PC×PD,
∵AQ切⊙O1于Q,APB是⊙O1的割线,
∴AQ2=AP×AB,
∴AQ2-AP2=AP×AB-AP2=AP(AB-AP)=AP×BP=PC•PD,
即AQ2-AP2=PC•PD.
点评:本题考查了相似三角形的性质和判定,圆内接四边形的性质,等腰三角形的性质,平行线分线段成比例定理等知识点的应用,主要考查学生综合运用性质进行推理的能力.

练习册系列答案
相关题目
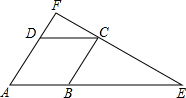 (1998•南京)已知:如图,菱形ABCD的边长为3,延长AB到点E,使BE=2AB,连接EC并延长交AD的延长线于点F.求AF的长.
(1998•南京)已知:如图,菱形ABCD的边长为3,延长AB到点E,使BE=2AB,连接EC并延长交AD的延长线于点F.求AF的长.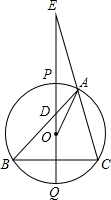 (1998•南京)已知:如图,△ABC内接于⊙O,过圆心O作BC的垂线交⊙O于点P、Q,交AB于点D,QP、CA的延长线交于点E.求证:OA2=OD•OE.
(1998•南京)已知:如图,△ABC内接于⊙O,过圆心O作BC的垂线交⊙O于点P、Q,交AB于点D,QP、CA的延长线交于点E.求证:OA2=OD•OE. (1998•南京)已知:如图,点P在∠AOB的边OA上.
(1998•南京)已知:如图,点P在∠AOB的边OA上.