题目内容
【题目】如图,⊙O是△ABC的外接圆,∠ABC=45°,AD是⊙O的切线交BC的延长线于D,AB交OC于E.

(1)求证:AD∥OC;
(2)若AE=2![]() ,CE=2.求⊙O的半径和线段BE的长.
,CE=2.求⊙O的半径和线段BE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连结OA,根据切线的性质得到OA⊥AD,再根据圆周角定理得到∠AOC=2∠ABC=90°,然后根据平行线的判定即可得到结论;
(2)设⊙O的半径为R,则OA=R,OE=R-2,AE=2![]() ,在Rt△OAE中根据勾股定理可计算出R=4;作OH⊥AB于H,根据垂径定理得AH=BH,再利用面积法计算出OH=
,在Rt△OAE中根据勾股定理可计算出R=4;作OH⊥AB于H,根据垂径定理得AH=BH,再利用面积法计算出OH=![]() ,然后根据勾股定理计算出AH=
,然后根据勾股定理计算出AH=![]() ,则HE=AE-AH=2
,则HE=AE-AH=2![]() -
-![]() =
=![]() ,再利用BE=BH-HE进行计算.
,再利用BE=BH-HE进行计算.
试题解析:(1)连结OA,如图,
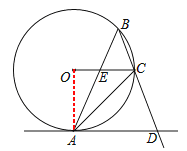
∵AD是⊙O的切线,
∴OA⊥AD,
∵∠AOC=2∠ABC=2×45°=90°,
∴OA⊥OC,
∴AD∥OC;
(2)设⊙O的半径为R,则OA=R,OE=R-2,AE=2![]() ,
,
在Rt△OAE中,∵AO2+OE2=AE2,
∴R2+(R-2)2=(2![]() )2,解得R=4,
)2,解得R=4,
作OH⊥AB于H,如图,OE=OC-CE=4-2=2,
则AH=BH,
∵![]() OHAE=
OHAE=![]() OEOA,
OEOA,
∴OH=![]() =
=![]() ,
,
在Rt△AOH中,AH=![]() ,
,
∴HE=AE-AH=2![]() -
-![]() =
=![]()
∴BH=![]() ,
,
∴BE=BH-HE=![]() -
-=
![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
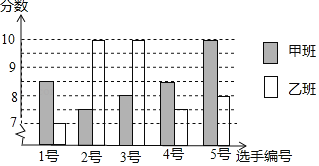
小学生10分钟应用题系列答案【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班
分别选5名同学参加“国防知识”比赛,
其预赛成绩如图所示:
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | |
甲班 | 8.5 | 8.5 |
|
乙班 | 8.5 |
| 10 |
(2)分别求甲乙两班的方差,并从稳定性上分析哪个班的成绩较好.