��Ŀ����
����Ŀ����ѧ�
(1)�龳�۲�
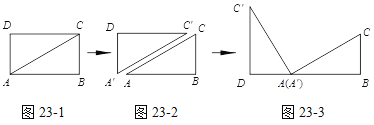
������ֽƬABCD�ضԽ���AC�������õ���ABC�͡�A��C��D����ͼ23-1��ʾ.����A��C��D�Ķ���A�����A�غϣ����Ƶ�A(A��)����ʱ�뷽����ת��ʹ��D��A(A��)��B��ͬһ��ֱ���ϣ���ͼ23-2��ʾ��
�۲�ͼ23-2��֪����BC��ȵ��߶��� ����CAC��= �ȣ�
(2)����̽��
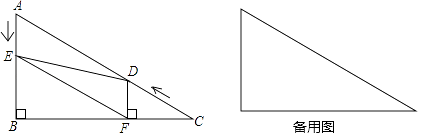
��ͼ23-3����ABC�У�AG��BC�ڵ�G����AΪֱ�Ƕ��㣬�ֱ���AB��ACΪֱ�DZߣ����ABC��������Rt��ABE�͵���Rt��ACF������E��F������GA�Ĵ��ߣ�����ֱ�ΪP��Q. ��̽��EP��FQ֮���������ϵ����֤����Ľ���.
(3)��չ����
��ͼ23-4����ABC�У�AG��BC�ڵ�G���ֱ���AB��ACΪһ�����ABC��������ABME�;���ACNF������GA��EF�ڵ�H. ��AB=k��AE��AC=k��AF����̽��HE��HF֮���������ϵ����˵������.
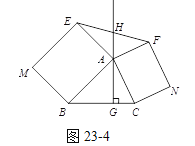
���𰸡���1��DA��90����2��FQ=EP��֤�����£���3��HE=HF����������.
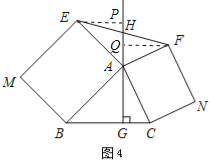
���������⣺��1����ͼ2������ת�����ʿ�֪����ABC�ա�A��C��D��
��BC=A��D����ACB=��C��AD������ACB+��CAB=90����
���C��AD+��CAB=90��������CAC��=90����
�ʴ�Ϊ��A��D��=90����
��2��EP=FQ��
֤�����ߡ�ABE�ǵ���ֱ�������Σ�
���EAB=90��������EAP+��BAG=90��������ABG+��BAG=90����
���EAP=��ABG��
����APE����BGA��
![]() ��
��
���APE�ա�BGA��
��EP=AG��
ͬ����FQ=AG��
��EP=FQ��
��3��HE=HF��
֤������EP��GA��GA���ӳ�����P����FQ��GA��GA���ӳ�����Q��
���ı���ABME�Ǿ��Σ�
���EAB=90��������EAP+��BAG=90��������ABG+��BAG=90����
���EAP=��ABG������APE=��BGA=90����
���APE�ס�BGA��
��![]() =����AG=kEP��
=����AG=kEP��
ͬ����AQF�ס�CGA��
��![]() =k����AG=kFQ��
=k����AG=kFQ��
��EP=FQ��
��EP��GA��FQ��GA��
��EP��FQ����EP=FQ��
��HE=HF��

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�