题目内容
【题目】如图,在平面直角坐标系xOy中,已知点A(﹣1,0),点B(0,2),点C(3,0),直线a为过点D(0,﹣1)且平行于x轴的直线. 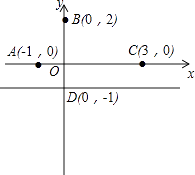
(1)直接写出点B关于直线a对称的点E的坐标;
(2)若P为直线a上一动点,请求出△PBA周长的最小值和此时P点坐标;
(3)若M为直线a上一动点,且S△ABC=S△MAB , 请求出M点坐标.
【答案】
(1)(0,﹣4)
(2)解:∵B、E关于直线a对称,
∴PB=PE,
∴△PBA周长=AB+BP+PA
=AB+PE+PA
∵两点之间线段最段,
∴△PBA周长的最小值=AB+AE= ![]() ,
,
∴直线AE的解析式:y=﹣4x﹣4,
当y=﹣1时,x= ![]() ,
,
∴P点坐标( ![]() ,﹣1)
,﹣1)
(3)解:设M(m,﹣1),
当M在第四象限,
∵S△ABC=S△MAB,
∴点M在过C且平行于AB的直线上,
∵直线AB的解析式为:y=2x+2,
设直线CM的解析式为:y=2x+n,
∴0=2×3+n,
∴n=﹣6,
∴直线CM的解析式为:y=2x﹣6,
∴m= ![]() ,
,
∴M( ![]() ,﹣1),
,﹣1),
当M在第三象限,
直线AB与直线a交于G(﹣ ![]() ,﹣1),
,﹣1),
∴ ![]() ×(﹣
×(﹣ ![]() ﹣m)×(2+1)﹣
﹣m)×(2+1)﹣ ![]() ×(﹣
×(﹣ ![]() ﹣m)×1=
﹣m)×1= ![]() ×4×2,
×4×2,
∴m=﹣5.5,
∴M(﹣5.5,﹣1).

【解析】解:(1)∵B(0,2),D(0,﹣1), ∴BD=3,
∵直线a为过点D(0,﹣1)且平行于x轴的直线.
∴BD⊥直线a,
∴点B关于直线a对称的点E的坐标(0,﹣4);
所以答案是:(0,﹣4);
【考点精析】利用轴对称-最短路线问题对题目进行判断即可得到答案,需要熟知已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目