题目内容
【题目】如图，矩形ABCD的对角线AC、BD交于点O，CE∥BD，DE∥AC．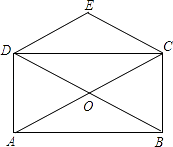 
（1）证明：四边形OCED为菱形；
（2）若AC=4，求四边形CODE的周长．
【答案】
（1）解：证明：∵CE∥BD，DE∥AC，
∴四边形CODE为平行四边形
又∵四边形 ABCD 是矩形
∴OD=OC
∴四边形CODE为菱形
（2）解：∵四边形 ABCD 是矩形
∴OC=OD= 
AC
又∵AC=4
∴OC=2
由（1）知，四边形CODE为菱形
∴四边形CODE的周长为=4OC=2×4=8．
【解析】（1）首先由CE∥BD，DE∥AC，可证得四边形CODE是平行四边形，又由四边形ABCD是矩形，根据矩形的性质，易得OC=OD，即可判定四边形CODE是菱形，（2）求出OC=OD=2，由菱形的性质即可得出答案．
【考点精析】认真审题，首先需要了解矩形的性质(矩形的四个角都是直角，矩形的对角线相等)．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
【题目】学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛，在选拔过程中，每人射击10次，计算他们的平均成绩及方差如下表：
选手 | 甲 | 乙 |
平均数（环） | 9.5 | 9.5 |
方差 | 0.035 | 0.015 |
请你根据上表中的数据选一人参加比赛，最适合的人选是 ．
