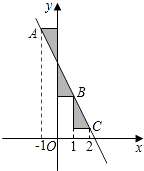Question

【题目】如图，在平面直角坐标系中，点A(－1，0)，B(0，2)，点C在x轴上，且∠ABC＝90°.

(1)求点C的坐标；

(2)求经过A，B，C三点的抛物线的表达式；

(3)在(2)中的抛物线上是否存在点P，使∠PAC＝∠BCO？若存在，求出点P的坐标；若不存在，说明理由．

Answer 1

【答案】（1）（4，0）（2）y=；（3）（3，2），（5，-3）

【解析】试题分析：（1）设点C 的坐标为（x，0），在直角三角形ABC中运用勾股定理即可求出x的值，从而确定点C的坐标；

（2）设出二次函数关系式，把A、B、C三点坐标代入求解即可；

（3） 存在，利用正切值相等，分两种情况列式计算即可.

试题解析：（1）设C（x，0）（x>0）

∴AC=x+1，BC=，AB=

∵∠ABC＝90°

∴AB2+BC2=AC2

∴5+x2+4=(x+1)2

解得：x=4

∴C（4,0）

(2)∵A(－1，0)，B(0，2)，C(4,0)

设抛物线的解析式为：y=a(x+1)(x-4)

把点B（0，2）代入上式得：a=

∴抛物线的解析式为：y= (x+1)(x-4)= x2+x+2;

(3)∵∠PAC=∠BCO

∴tan∠PAC=tan∠BCO

∴tan∠PAC=tan∠BCO=

设P点坐标为（x，y）

当点P在x轴上方时，y>0

∴tan∠PAC=

联立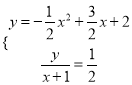

∴x2-2x-3=0

∵y>0

∴x=3

∴点P坐标为（3，2）

当点P在x轴下方时，y<0，x>0

∴tan∠PAC=

联立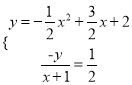

∴x2-4x-5=0

∵y<0

∴x=-5

∴点P坐标为（-5，3）

综上可得：点P的坐标为（3，2）或（-5，3）.