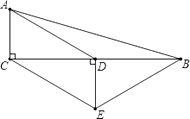
题目内容
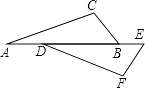
【题目】已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.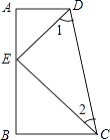
【答案】解:∵CE平分∠BCD,DE平分∠CDA,
∴∠1= ![]() ∠ADC,∠2=
∠ADC,∠2= ![]() ∠BCD,
∠BCD,
∴∠1+∠2= ![]() ∠ADC+
∠ADC+ ![]() ∠BCD=
∠BCD= ![]() (∠ADC+∠BCD)=90°,
(∠ADC+∠BCD)=90°,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∴∠A+∠B=180°,
∵CB⊥AB,
∴∠A=90°,
∴DA⊥AB.
【解析】根据角平分线定义和∠1+∠2=90°,得到∠ADC+∠BCD=180°,根据同旁内角互补,两直线平行;得到AD∥BC,再根据两直线平行,同旁内角互补,得到DA⊥AB.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目