题目内容
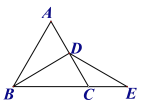
【题目】如图，使ΔABC≌ΔADC成立的条件是（ ）
A.AB=AD，∠B=∠DB.AB=AD，∠ACB=ACD
C.BC=DC，∠BAC=∠DACD.AB=AD，∠BAC=∠DAC
【答案】D
【解析】
两个三角形已经有一条公共边AC，将此条件与每个选项的条件结合，根据全等三角形的判定定理，逐项判断是否能够判定ΔABC≌ΔADC.
A．AC=AC，AB=AD，∠B=∠D三个条件构成“边边角”，不能判定ΔABC≌ΔADC；
B．AB=AD，AC=AC，∠ACB=∠ACD三个条件构成“边边角”，不能判定ΔABC≌ΔADC；
C．BC=AD，AC=AC，∠BAC=∠DAC三个条件构成“边边角”，不能判定ΔABC≌ΔADC；
D．AB=AD，∠BAC=∠DAC，AC=AC三个条件构成“边角边”，可以判定ΔABC≌ΔADC；
故选D.
练习册系列答案
名校课堂系列答案
相关题目
【题目】抛物线
上部分点的横坐标x，纵坐标y的对应值如下表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法正确的个数是（ ）
①抛物线与x轴的一个交点为（﹣2，0）；②抛物线与y轴的交点为（0，6）；
③抛物线的对称轴是x=1；④在对称轴左侧y随x增大而增大．
A. 1 B. 2 C. 3 D. 4
