Question

如图，在边长为l的小正方体组成的网格中，小正方体的顶点称为格点，△ABC的三个顶点都在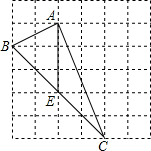格点上．
（1）在网格中确定一点D，使得

AB

=

CD

（只要画出向量，不必写作法）；
（2）若E为BC的中点，则tan∠CAE=

 

；
（3）在△ACD中，求∠CAD的正弦值．

Answer 1

分析：（1）首先根据平行四边形法则，即可画出图形；
（2）延长AE到K，使得AK⊥CK，由tan∠CAE=

CK

AK

，即可求得答案；
（3）首先由AC=

52+22

=

29

，DC=

5

，AD=

32

，可得△ACD不是直角三角形，然后作DM⊥AC于M，利用三角形的面积求得AC边上的高，继而可求得∠CAD的正弦值．

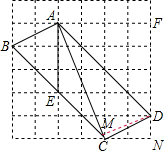
解答：解：（1）如图：点D即为所求；


（2）如图：根据题意可知：
tan∠CAE=

CK

AK

=

2

5

．
故答案为：

2

5

；

（3）根据题意得：AC=

52+22

=

29

，DC=

5

，AD=

32

，
∴△ACD不是直角三角形，
作DM⊥AC于M，
S_△ADC=S_梯形AFNC-S_△AFD-S_△CND，
=

1

2

（AF+CN）•FN-

1

2

AF•DF-

1

2

DN•CN，
=

1

2

×（4+2）×5-

1

2

×4×4-

1

2

×2×1，
=6，
S_△ADC=

1

2

•AC•DM=

1

2

×

29

×DM=6，
∴DM=

12

29

，
在Rt△ADM中，sin∠CAD=

DM

AD

=

12

29

÷

32

=

3 58

58

．

点评：此题考查了平面向量的知识，三角函数以及三角形面积的求解方法等知识．此题难度较大，解题的关键是注意数形结合思想的应用．